A couple of days back, I wrote about kernels and why the kernel trick is called a “trick.”
To recap, the kernel provides a way to compute the dot product between two vectors, X and Y, in some high-dimensional space without projecting the vectors to that space.
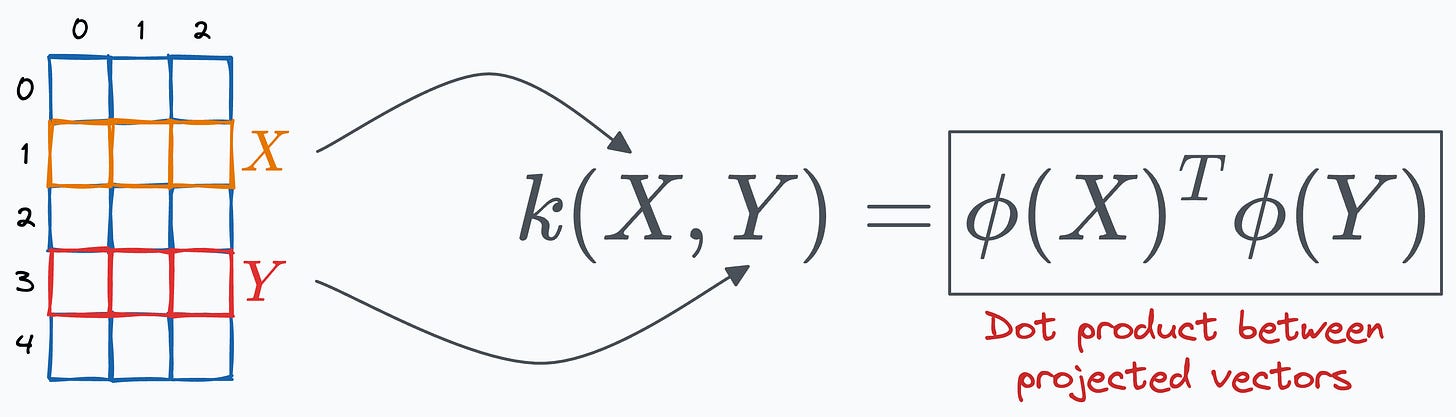
In that post, we looked at the polynomial kernel and saw that it computes the dot product of a 2-dimensional vector in a 6-dimensional space without explicitly visiting that space.
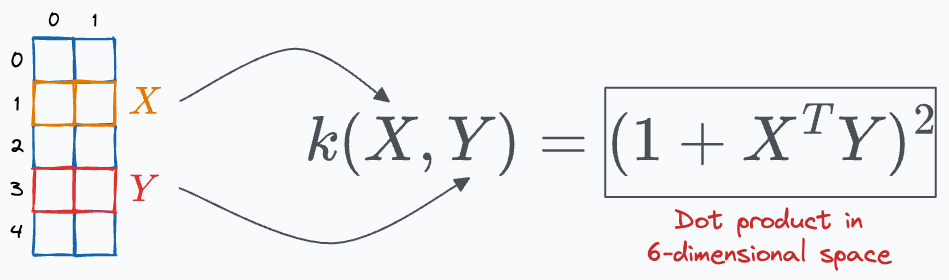
Today, I want to continue that discussion and talk about the RBF kernel, another insanely powerful kernel, which is also the default kernel in a support vector classifier class implemented by sklearn:

To begin, the mathematical expression of the RBF kernel is depicted below (and consider that we have just a 1-dimensional feature vector):
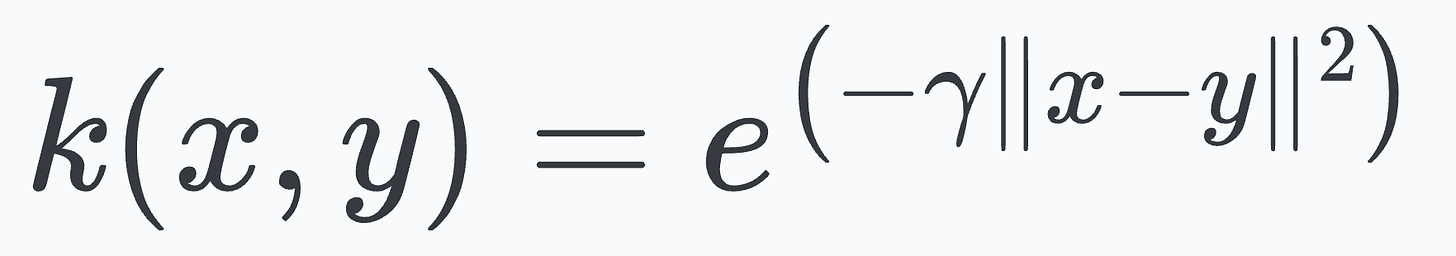
You may remember from high school mathematics that the exponential function is defined as follows:
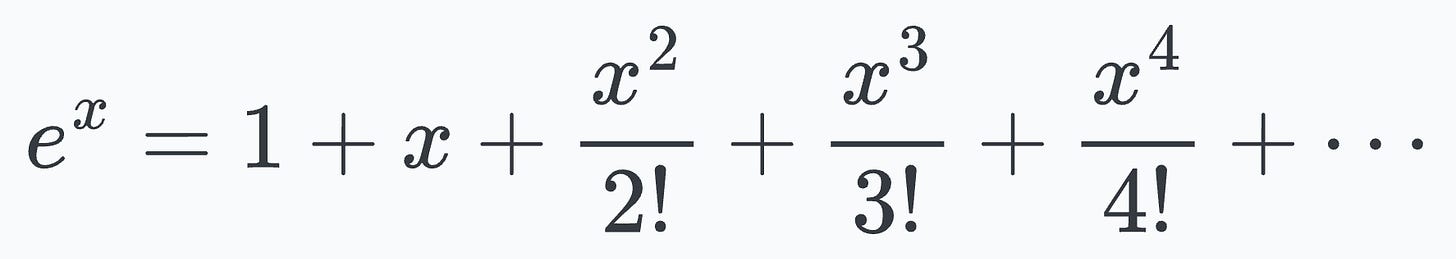
Expanding the square term in the RBF kernel expression, we get:
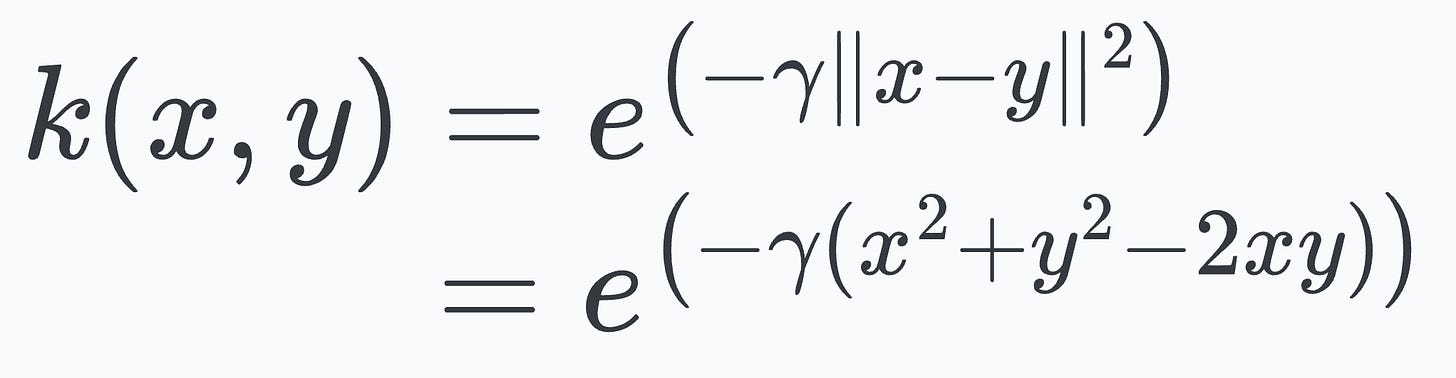
Distributing the gamma term and expanding the exponential term using the exponent rule, we get:
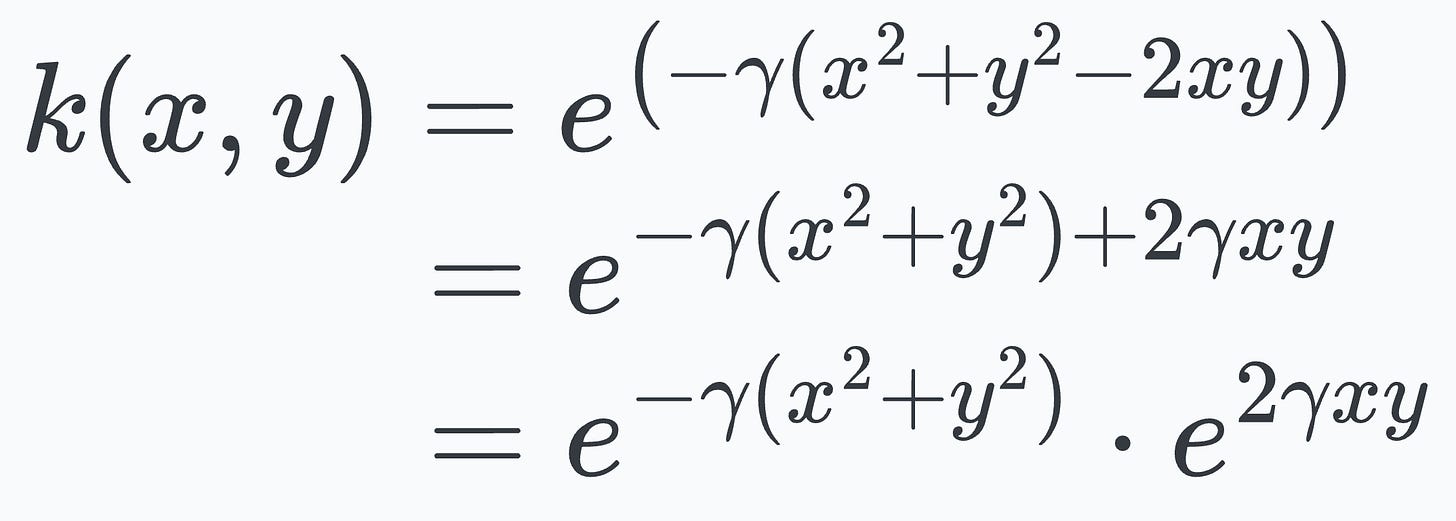
Next, we apply the exponential expansion to the last term and get the following:
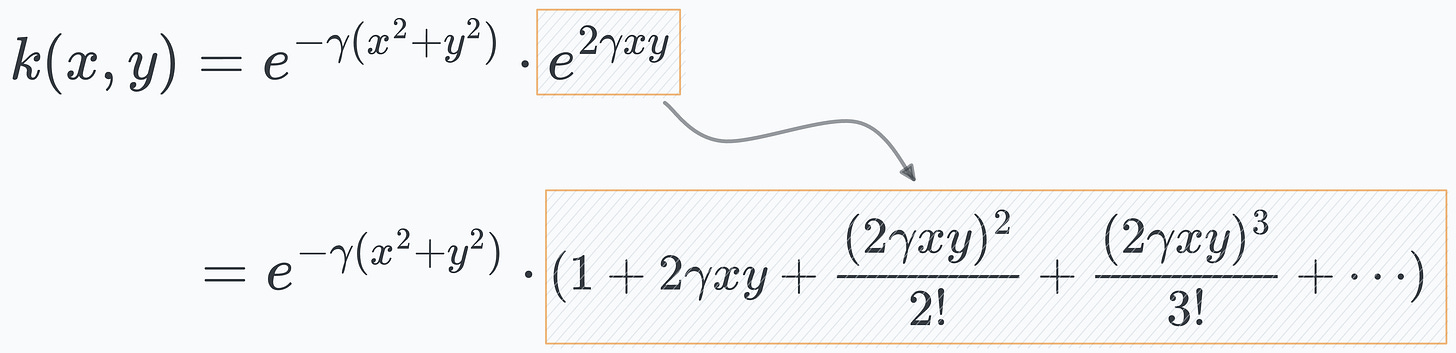
Almost done.
Notice closely that the exponential expansion above can be rewritten as the dot product between the following two vectors:

And there you go.
We get our projection function:
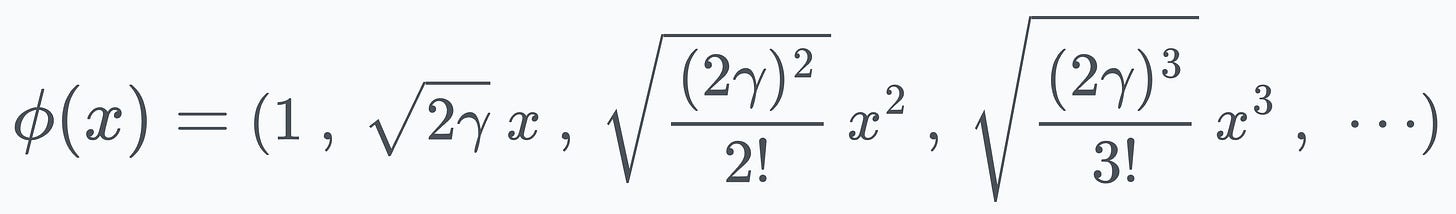
It is evident that this function maps the 1-dimensional input to an infinite-dimensional feature space.
This shows that the RBF kernel function we chose earlier computes the dot product in an infinite-dimensional space without explicitly visiting that space.
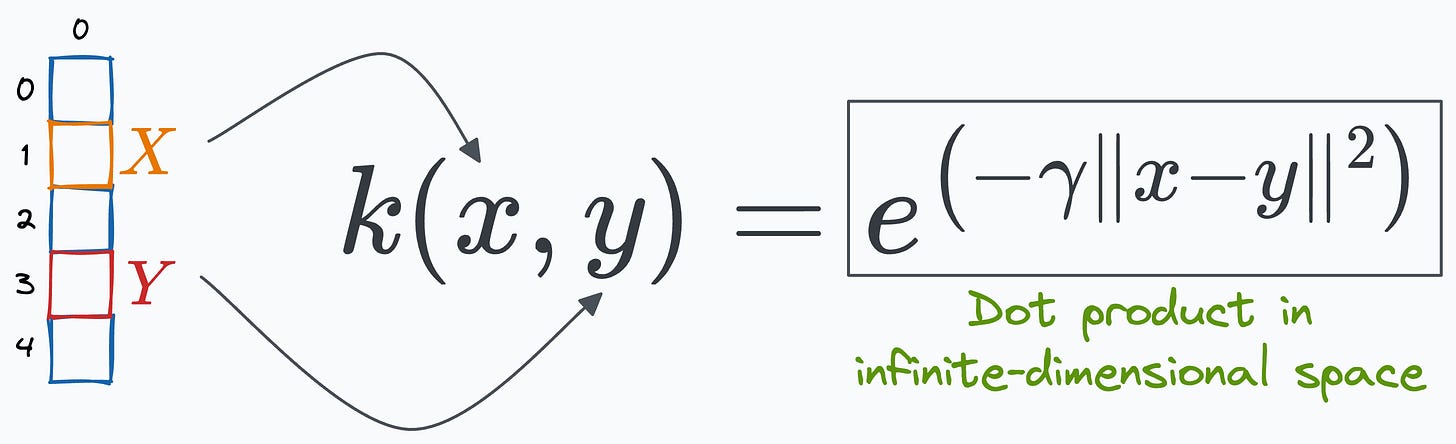
This is why the RBF kernel is considered so powerful, allowing it to easily model highly complex decision boundaries.
Here, I want to remind you that even though the kernel is equivalent to the dot product between two infinite-dimensional vectors, we NEVER compute that dot product, so the computation complexity is never compromised.
That is why the kernel trick is called a “trick.” In other words, it allows us to operate in high-dimensional spaces without explicitly computing the coordinates of the data in that space.
Isn’t that cool?
Did you like the mathematical details here? If yes, we covered the mathematical foundations in such an intuitive and beginner-friendly way of many concepts here:
- Why Bagging is So Ridiculously Effective At Variance Reduction?
- Formulating and Implementing the t-SNE Algorithm From Scratch
- The Probabilistic Origin of Regularization
- Why Sklearn’s Logistic Regression Has No Learning Rate Hyperparameter?
- You Are Probably Building Inconsistent Classification Models Without Even Realizing
👉 Over to you: Can you tell a major pain point of the kernel trick algorithms?






