You Are Probably Building Inconsistent Classification Models Without Even Realizing

👉

Introduction

As you may already know, the primary objective of building classification models is to categorize data points into predefined classes or labels based on the input features.

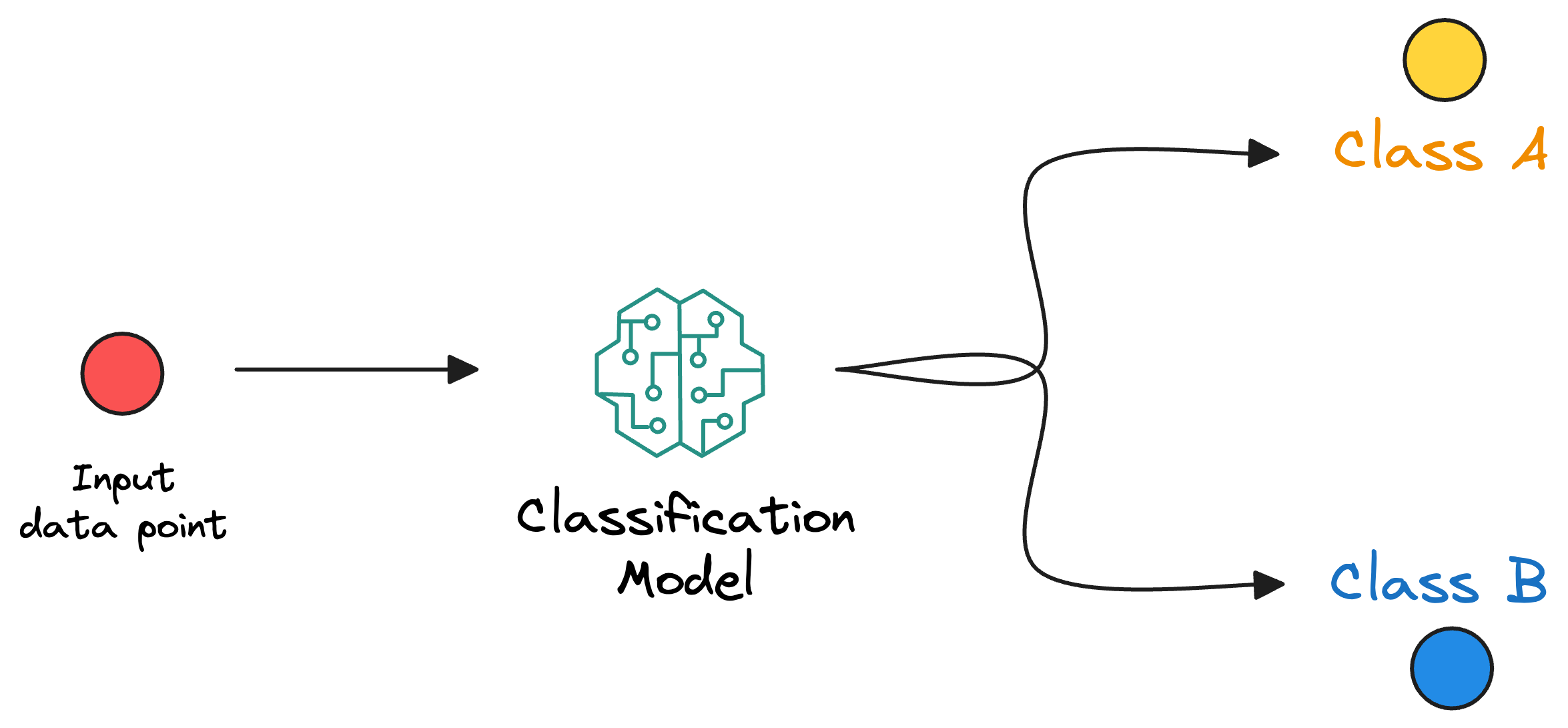
More technically speaking, the objective is to learn a function $f$ that maps an input vector (x) to a label (y).

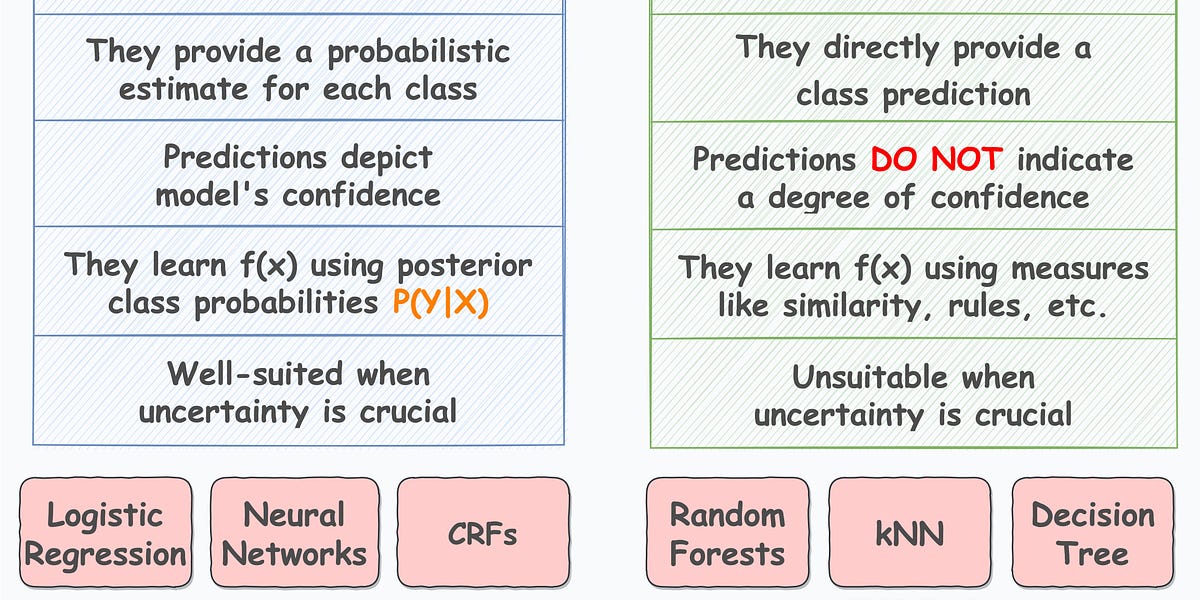
They can be further divided into two categories:

Probabilistic models: These models output a probabilistic estimate for each class.
Direct labeling models: These models directly predict the class label without providing probabilistic estimates.

We have already discussed this in the newsletter recently, so we won’t get into much detail again:

Moving on...

Talking specifically about neural networks (which are probabilistic models), the model is typically trained with the cross-entropy loss function, as shown below:

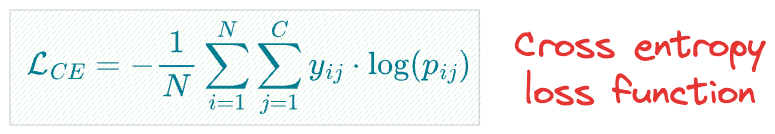
where:

$N$ is the number of samples in the dataset.
$C$ is the number of classes.
$y_{ij}$ is an indicator variable that equals $1$ if the $i^{th}$ sample belongs to class $j$, and $0$ otherwise.
$p_{ij}$ is the predicted probability that the $i^{th}$ sample belongs to class $j$ according to the model.

If it is getting difficult to understand this loss function, just think of it as the sum of the log-loss (binary classification loss function) over every class.

While cross-entropy is undoubtedly one of the most used loss functions for training multiclass classification models, it is not entirely suitable in certain situations.

More specifically, in many real-world classification tasks, the class labels often possess a relative ordering between them.

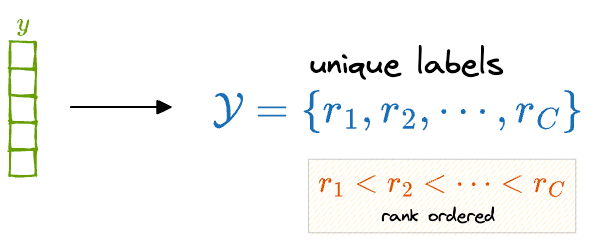
For instance, consider an age detection task where the goal is to predict the age group of individuals based on facial features:

In such a scenario, the class labels typically represent age ranges or groups, such as child, teenager, young adult, middle-aged, and senior. These age groups inherently possess an ordered relationship, where child precedes teenager, teenager precedes young adult and so on.

Traditional classification approaches, such as cross-entropy loss, treat each age group as a separate and independent category. Thus, they fail to capture the underlying ordinal relationships between the age groups.

Consequently, the model might struggle to differentiate between adjacent age groups, leading to suboptimal performance and classifier ranking inconsistencies.

By "ranking inconsistencies," we mean those situations where the predicted probabilities assigned to adjacent age groups do not align with their natural ordering.

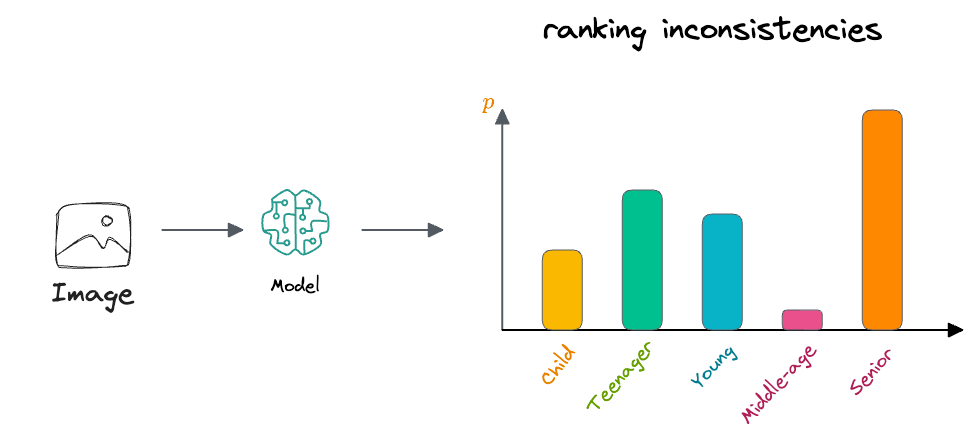
For example, if the model predicts a lower probability for the child age group than for the teenager age group, despite the fact that teenager logically follows child in the age hierarchy, this would constitute a ranking inconsistency.

We could also interpret it in this way that, say, the true label for an input sample is young adult. Then in that case, we would want our classifier to highlight that the input sample is "at least a child", "at least a teenager", and "at least a young adult".

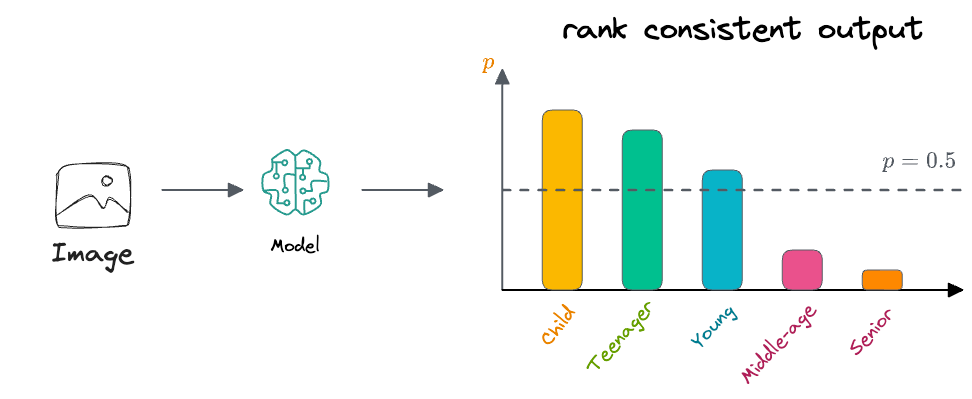
Beyond that, it may start outputting low probabilities for other age groups, as depicted above.

However, these inconsistencies are largely observed when we use cross-entropy loss. They arise due to the lack of explicit consideration for the ordinal relationships between age groups in traditional classification approaches.

Since cross-entropy loss treats each age group as a separate category with no inherent order, the model may struggle to learn and generalize the correct progression of age.

As a result, the model may exhibit inconsistent ranking behavior, where it assigns higher probabilities to age groups that logically should have lower precedence according to the age hierarchy.

This inconsistency not only undermines the interpretability of the model but also compromises its predictive accuracy, especially in scenarios where precise age estimation is crucial.

Here, we must note that ordinal classification techniques are not limited to age but are applicable across a wide range of domains where class labels exhibit inherent ordering.

Here are some more use cases:

Product Reviews: In sentiment analysis of product reviews, sentiment labels such as excellent, good, average, poor, and terrible represent an ordered ranking of the overall sentiment expressed in the reviews.
Economic Indicators: In economic forecasting, indicators such as strong growth, moderate growth, stagnation, recession, and depression represent an ordered ranking of economic conditions.
Risk Assessment: Risk assessment models may categorize risks into ordered levels such as low risk, medium risk, and high risk, based on the likelihood and impact of potential events.
Education Grading: In educational assessment, students' performance levels are often categorized based on grades, such as A, B, C, D, and F. These grades represent an ordered ranking from highest to lowest performance.
And many many more.

These examples illustrate how rank ordinal classification is prevalent across various domains.

Coming back...

The discussion so far indicates that we want our model to accurately classify data points into different categories and understand and respect the natural order or hierarchy present in the labels, which must also be respected during inference time.

However, as discussed above, commonly used loss functions like multi-category cross-entropy do not explicitly capture this ordinal information.

Ordinal classification

As the name suggests, ordinal classification involves predicting labels on an ordinal scale.

More formally, the model is trained such that it learns a ranking rule that maps a data point $x$ to an ordered set $y$, where each element $y_i \in y$ represents a class or category, and the order of these elements reflects the ordinal relationship between them.

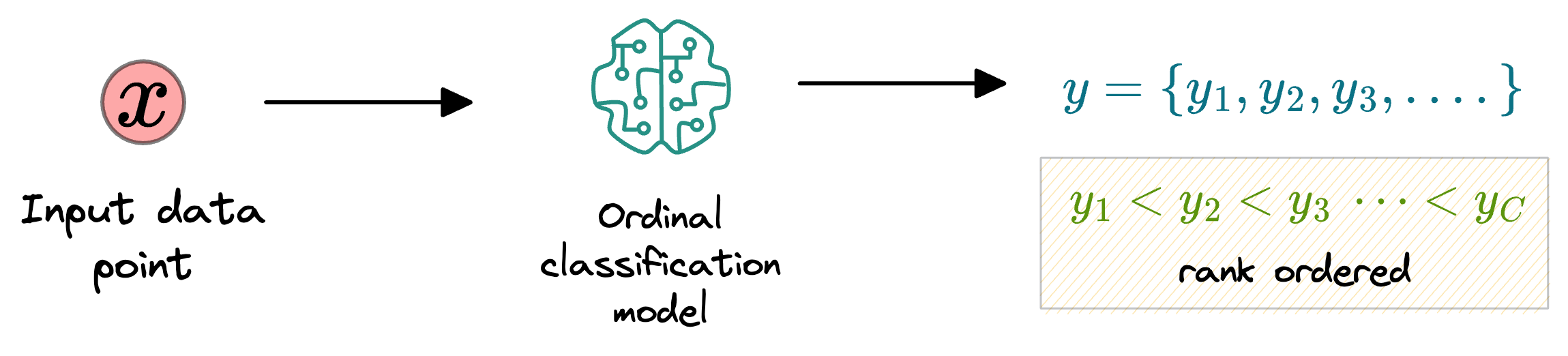
In ordinal classification, the focus shifts from simply assigning data points to discrete classes to understanding and respecting the relative order or hierarchy present in the classes.

As discussed above, this is particularly important in tasks where the classes exhibit a natural progression or ranking, such as age groups, severity levels, or performance categories.

The goal of ordinal classification is twofold:

first, to accurately predict the class labels for each data point,
and second, to ensure that these predictions adhere to the inherent order or ranking of the classes.

Achieving this requires specialized techniques and methodologies that go beyond traditional classification approaches.