Introduction
A common and fundamental way of training a logistic regression model, as taught in most lectures/blogs/tutorials, is using SGD.
Essentially, given an input $X$ and the model parameters $\theta$, the output probability ($\hat y$) is computed as follows:

Next, we compute the loss function ($J$), which is log-loss:
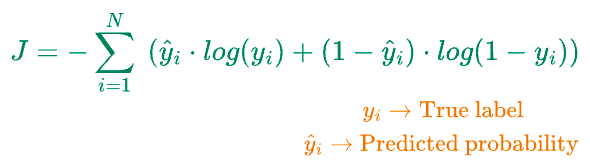
The final step is to update the parameters $\theta$ using gradient descent as follows:
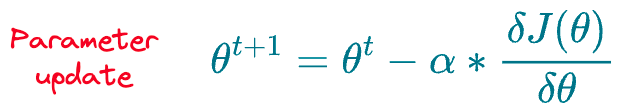
As depicted above, the weight update depends on the learning rate hyperparameter ($\alpha$), which we specify before training the model.
We execute the above steps (summarized again below) over and over for some epochs or until the parameter converges:
- Step 1) Initialize model parameters $\theta$.
- Step 2) Compute output probability $\hat y$ for all samples.
- Step 3) Compute the loss function $J(\theta)$, which is log-loss.
- Step 4) Update the parameters $\theta$ using gradient descent.
- Repeat steps 2-4 until convergence.
Simple, isn't it?
I am sure this is the method that you must also be thoroughly aware of.
However, if that is true, why don’t we see a learning rate hyperparameter $(\alpha)$ in the sklearn logistic regression implementation:
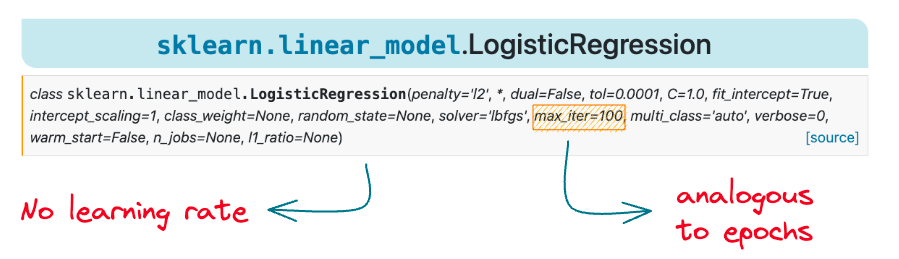
As depicted above, there is no learning rate parameter in this documentation.
However, we see a max_iter parameter that intuitively looks analogous to the epochs.
But how does that make sense?
We have epochs but no learning rate $\alpha$, so how do we even update the parameters of our model, as we do in SGD below?
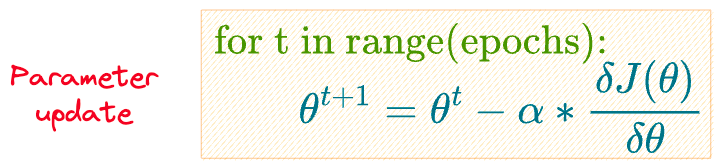
Are we missing something here?
As it turns out, we are indeed missing something here.
More specifically, there are a few more ways to train a logistic regression model, but most of us are only aware of the above SGD procedure, which depends on the learning rate.
But most of us never happen to consider them.
However, the importance of these alternate mechanisms is entirely reflected by the fact that even sklearn, one of the most popular libraries of data science and machine learning, DOES NOT use SGD in its logistic regression implementation.
Thus, in this article, I want to share the overlooked details of logistic regression and introduce you to one more way of training this model, which does not depend on the learning rate hyperparameter.
Let’s begin!
Background
Before understanding the alternative training mechanism of training logistic regression, it is immensely crucial to know how we model data while using logistic regression.
In other words, let’s understand how we frame its modeling mathematically.
Essentially, whenever we model data using logistic regression, the model is instructed to maximize the likelihood of observing the given data $(X, y)$.
More formally, a model attempts to find a specific set of parameters $\theta$ (also called model weights), which maximizes the following function:
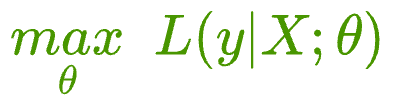
The above function $L$ is called the likelihood function, and in simple words, it says:
- maximize the likelihood of observing y
- given X
- when the prediction is parameterized by some parameters $\theta$ (also called weights)
When we begin modeling:
- We know $X$.
- We also know $y$.
- The only unknown is $\theta$, which we are trying to estimate.
Thus, the instructions given to the model are:
- Find the specific set of parameters $\theta$ that maximizes the likelihood of observing the data $(X, y)$.
This is commonly referred to as maximum likelihood estimation (MLE) in machine learning.
MLE is a method for estimating the parameters of a statistical model by maximizing the likelihood of the observed data.
It is a common approach for parameter estimation in various models, including linear regression, logistic regression, and many others.
The key idea behind MLE is to find the parameter values that make the observed data most probable.
The steps are simple and straightforward:
- Define the likelihood function for the entire dataset: Here, we typically assume that the observations are independent. Thus, the likelihood function for the entire dataset is the product of the individual likelihoods. Also, the likelihood function is parameterized by a set of parameters $\theta$, which are trying to estimate.
- Take the logarithm (the obtained function is called log-likelihood): To simplify calculations and avoid numerical issues, it is common to take the logarithm of the likelihood function.
- Maximize the log-likelihood: Finally, the goal is to find the set of parameters $\theta$, which maximizes the log-likelihood function.
In fact, it’s the MLE that helps us derive the log-loss used in logistic regression.
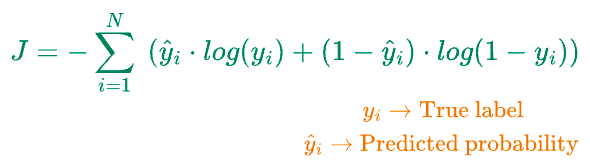
Formulating logistic regression MLE
We all know that in logistic regression, the model outputs the probability that a sample belongs to a specific class.
Let’s call it $\hat y$.
Assuming that you have a total of N independent samples $(X, y) = \{(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{N}, y_{N})\}$, the likelihood estimation can be written as:
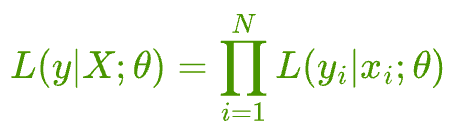
Essentially, we assume that all samples are independent.
Thus, the likelihood of observing the entire data is the same as the product of the likelihood of observing individual points.
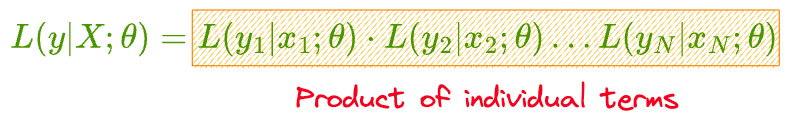
Next, we should determine these individual likelihoods $L(y_{i}|x_{i};\theta)$ as a function of the output probability of logistic regression $\hat y_i$:
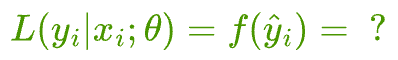
Logistic regression output to likelihood function conversion
While training logistic regression, the model returns a continuous output $\hat y$, representing the probability that a sample belongs to a specific class.
In logistic regression, the “specific class” is the one we have assigned the label of $y_{i} = 1$.
In other words, it is important to understand that a logistic regression model, by its very nature, outputs the probability that a sample belongs to one of the two classes.
More specifically, it is the class with true label $y_{i} = 1$.

The higher the output, the higher the probability that the sample has a true label $y_{i} = 1$.
Thus, we can say that when the true label $y_{i} = 1$, the likelihood of observing that data point is the output of logistic regression, i.e., $\hat y$.
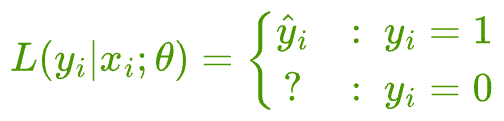
But how do we determine the likelihood when the true label $y_{i} = 0$?
For simplicity, consider the illustration below:
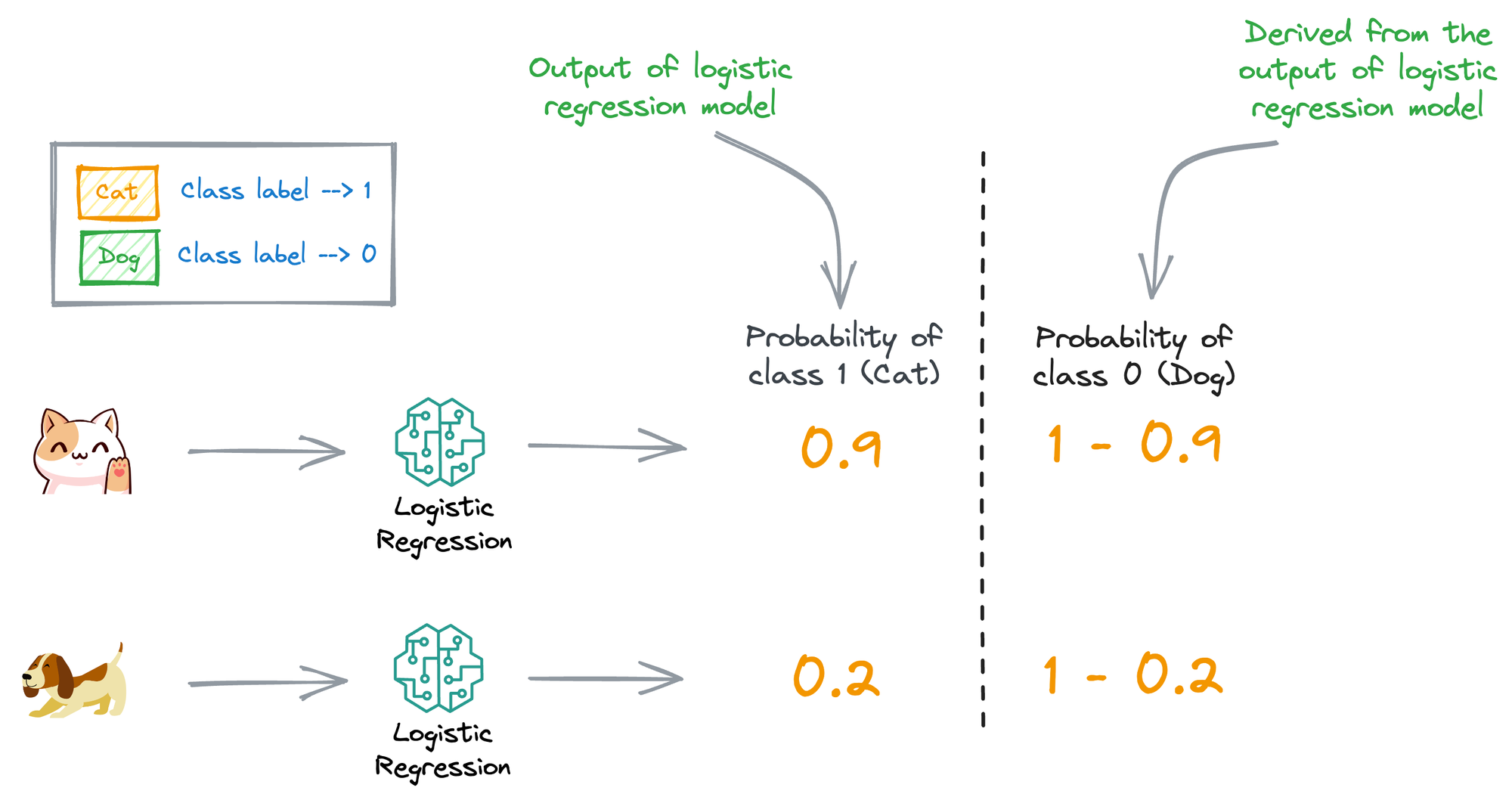
Assume that the label “Cat” is denoted as “Class 1” and the label “Dog” is denoted by “Class 0”.
Thus, all the logistic regression model outputs inherently denote the probability that an input is “Cat.”
But if we need the probability that the input is a “Dog,” we should take the complement of the output of the logistic regression model.
In other words, the likelihood when the true label $y_{i} = 0$ can be derived from the output of logistic regression $\hat y$.
Therefore, we get the following likelihood function for observing a specific data point $i$:
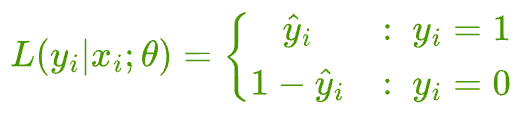
The likelihood of observing a sample with true label $y_{i} = 1$ is $\hat y_{i}$ (or the output of the model).
But the likelihood of observing a sample with true label $y_{i} = 0$ is $(1-\hat y_{i})$.
Final MLE step
We can dissolve the piecewise notation above to get the following:
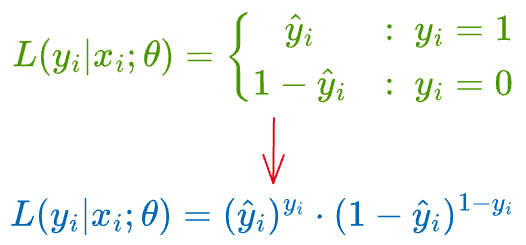
Let’s plug the likelihood function of individual data points back into the likelihood estimation for all samples:
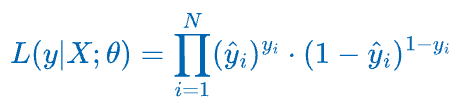
We can simplify the product to a summation by taking the logarithm on both sides.
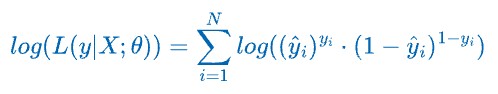
In practice, maximizing the log-likelihood function is often more convenient than the likelihood function.
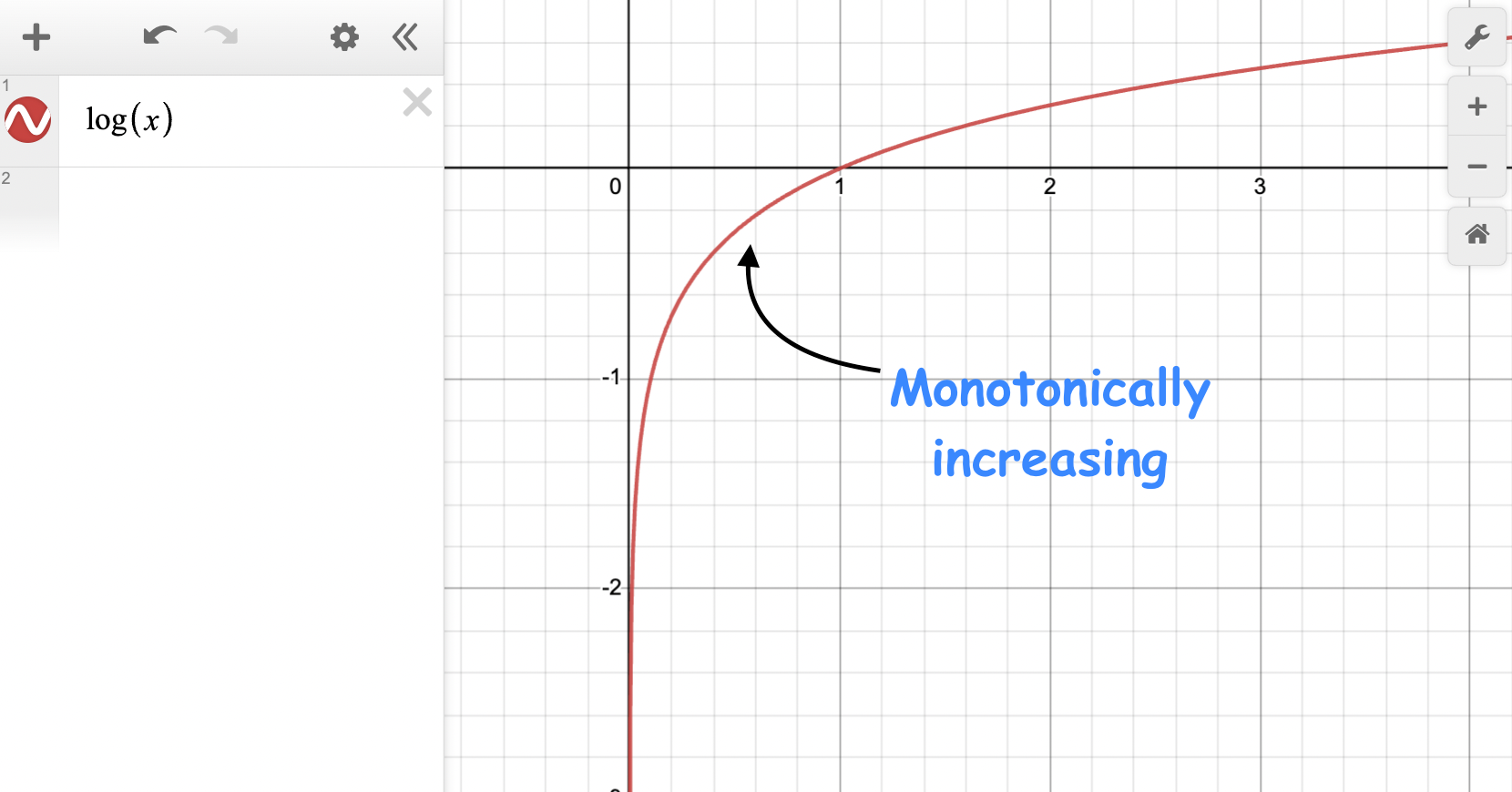
Since the logarithm is a monotonically increasing function, maximizing the log-likelihood is equivalent to maximizing the likelihood.
On further simplification, we get the following:
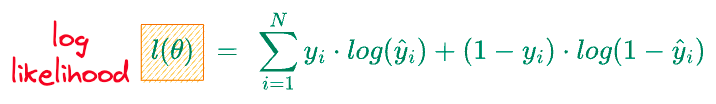
And to recall, $\hat y_i$ is the output probability by the logistic regression model:

The above derivation gave us the log-likelihood of the logistic regression model.
If we take negative (-) on both sides, it will give us the log loss, which can be conveniently minimized by gradient descent.
However, there is another way to manipulate the above log-likelihood formulation for more convenient optimization.
Let’s understand below.
Log-likelihood manipulation
Read the full article
Sign up now to read the full article and get access to all articles for paying subscribers only.
Join today!




