Why is Kernel Trick Called a "Trick"?

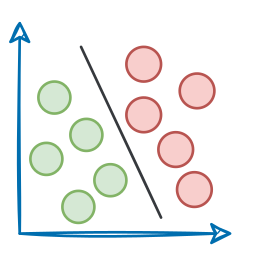
So many ML algorithms use kernels for robust modeling, like SVM, KernelPCA, etc.

In a gist, a kernel function lets us compute dot products in some other feature space (mostly high-dimensional) without even knowing the mapping from the current space to the other space.

But how does that even happen?

Let’s understand today!

The objective

Firstly, it is important to note that the kernel provides a way to compute the dot product between two vectors, X and Y, in some high-dimensional space without projecting the vectors to that space.

This is depicted below, where the output of the kernel function is expected to be the same as the dot product between projected vectors:

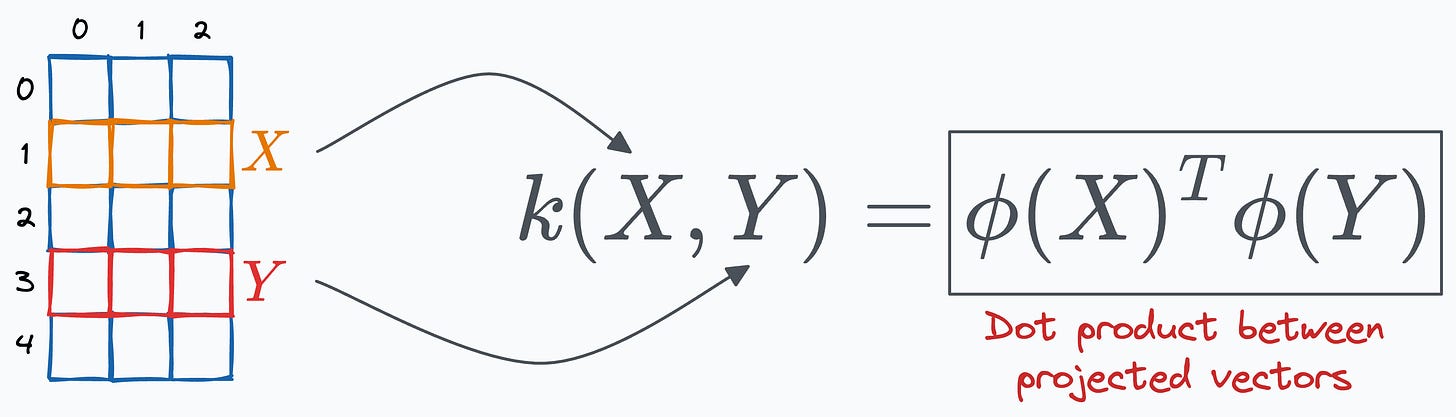
The key advantage is that the kernel function is applied to the vectors in the original feature space.

However, that equals the dot product between the two vectors when projected into a higher-dimensional (yet unknown) space.

If that is a bit confusing, let me give an example.

A motivating example

Let’s assume the following polynomial kernel function:

For simplicity, let’s say both X and Y are two-dimensional vectors:

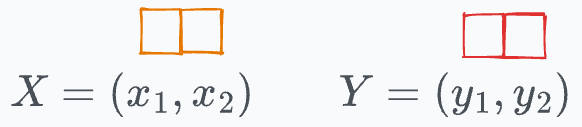
Simplifying the kernel expression above, we get the following:

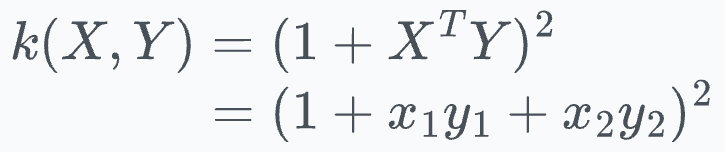
Expanding the square term, we get:

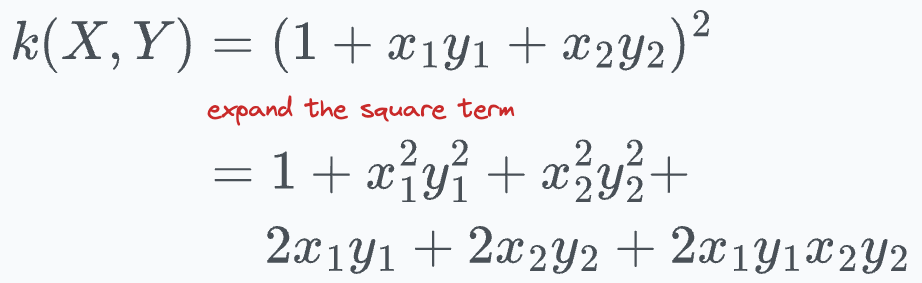
Now notice the final expression:

The above expression is the dot product between the following 6-dimensional vectors:

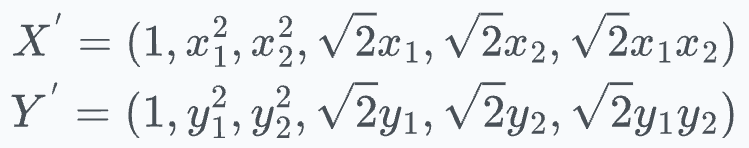
Thus, our projection function comes out to be:

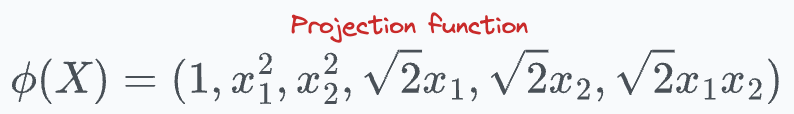
This shows that the kernel function we chose earlier computes the dot product in a 6-dimensional space without explicitly visiting that space.

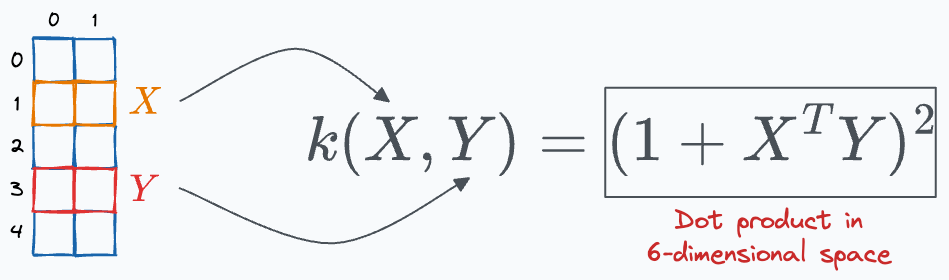
And that is the primary reason why we also call it the “kernel trick.”

More specifically, it’s framed as a “trick” since it allows us to operate in high-dimensional spaces without explicitly computing the coordinates of the data in that space.

Isn’t that cool?

The one we discussed above is the polynomial kernel, but there are many more kernel functions we typically use: