Introduction
In the pre-LLM era, whenever someone open-sourced any high-utility model for public use, in most cases, practitioners would fine-tune that model to their specific task.
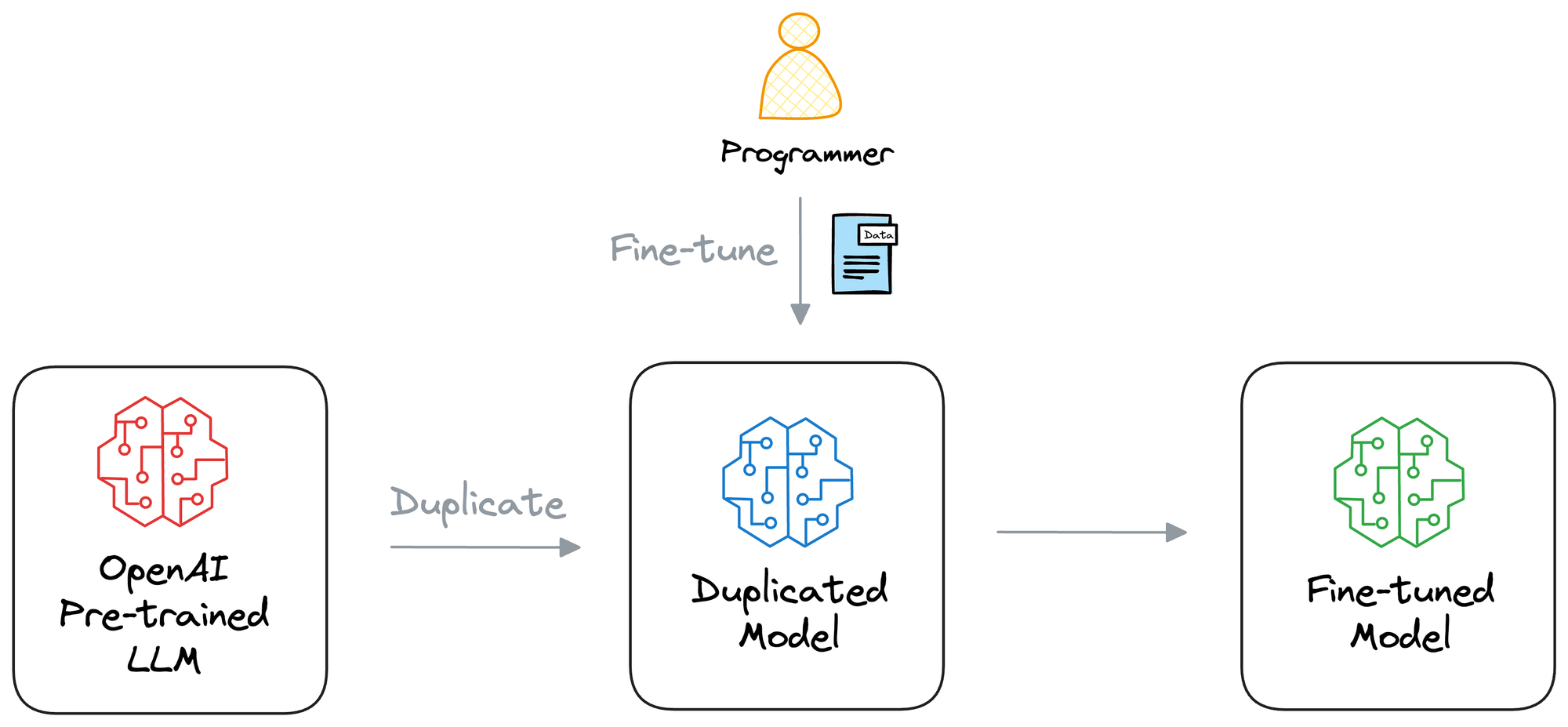
As also discussed in the most recent article on vector databases, fine-tuning means adjusting the weights of a pre-trained model on a new dataset for better performance. This is neatly depicted in the animation below:
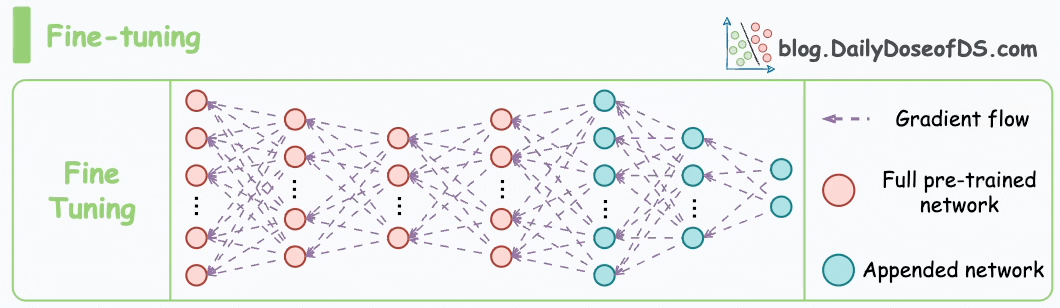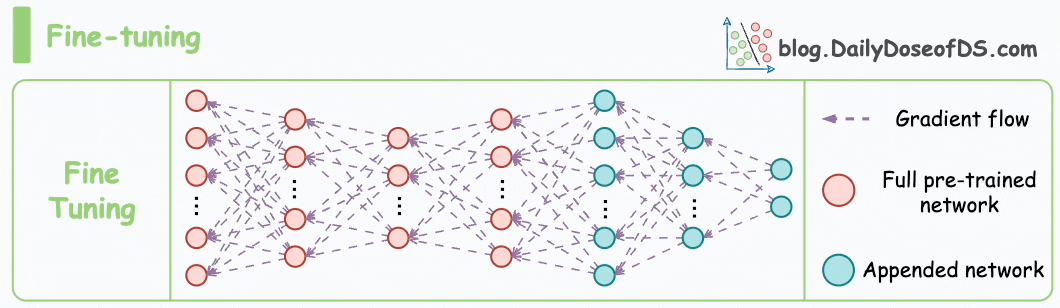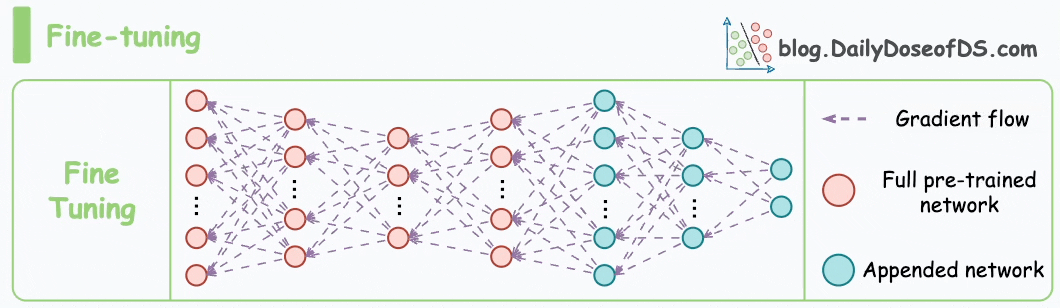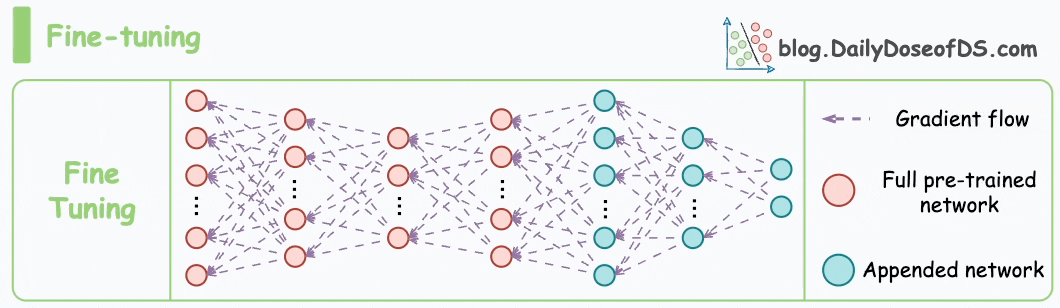
The motivation to do this is pretty simple.
When the model was developed, it was trained on a specific dataset that might not perfectly match the characteristics of the data a practitioner wants to use it on.
The original dataset might have had slightly different distributions, patterns, or levels of noise compared to the new dataset.
Fine-tuning allows the model to adapt to these differences, learning from the new data and adjusting its parameters to improve its performance on the specific task at hand.
For instance, consider BERT. It’s a Transformer-based language model, which is popularly used for text-to-embedding generation (92k+ citations on the original paper).
It’s open-source.
As we discussed in the vector database deep dive, BERT was pre-trained on a large corpus of text data, which might be very very different from what someone else may want to use it on.
Thus, when using it on any downstream task, we can adjust the weights of the BERT model along with the augmented layers, so that it better aligns with the nuances and specificities of the new dataset.

The idea makes total practical sense. In fact, it has been successfully used for a long time now, not just after the release of BERT but even prior to that.
However, the primary reason why fine-tuning has been pretty successful in the past is that we had not been training models that were ridiculously massive.
Talking of BERT again, it has two variants:
- BERT-Base, which has 110M parameters (or .11B).
- BERT-Large, which has 340M parameters (or .34B).
This size isn’t overwhelmingly large, which makes it quite feasible to fine-tune it on a variety of datasets without requiring immense computational resources.
Issues with fine-tuning
However, a problem arises when we use the same traditional fine-tuning technique on much larger models — LLMs, for instance.
This is because, as you may already know, these models are huge — billions or even trillions of parameters.
Consider GPT-3, for instance. It has 175B parameters, which is 510 times bigger than even the larger version of BERT called BERT-Large:
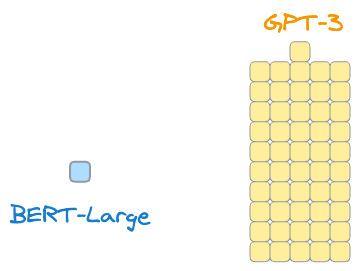
And to give you more perspective, I have successfully fine-tuned BERT-large in many of my projects on a single GPU cluster, like in this paper and this paper.
But it would have been impossible to do the same with GPT-3.
Moving on, while OpenAI has not revealed the exact number of parameters in GPT-4, it is suspected to be around 1.7 Trillion, which is roughly ten times bigger than GPT-3:
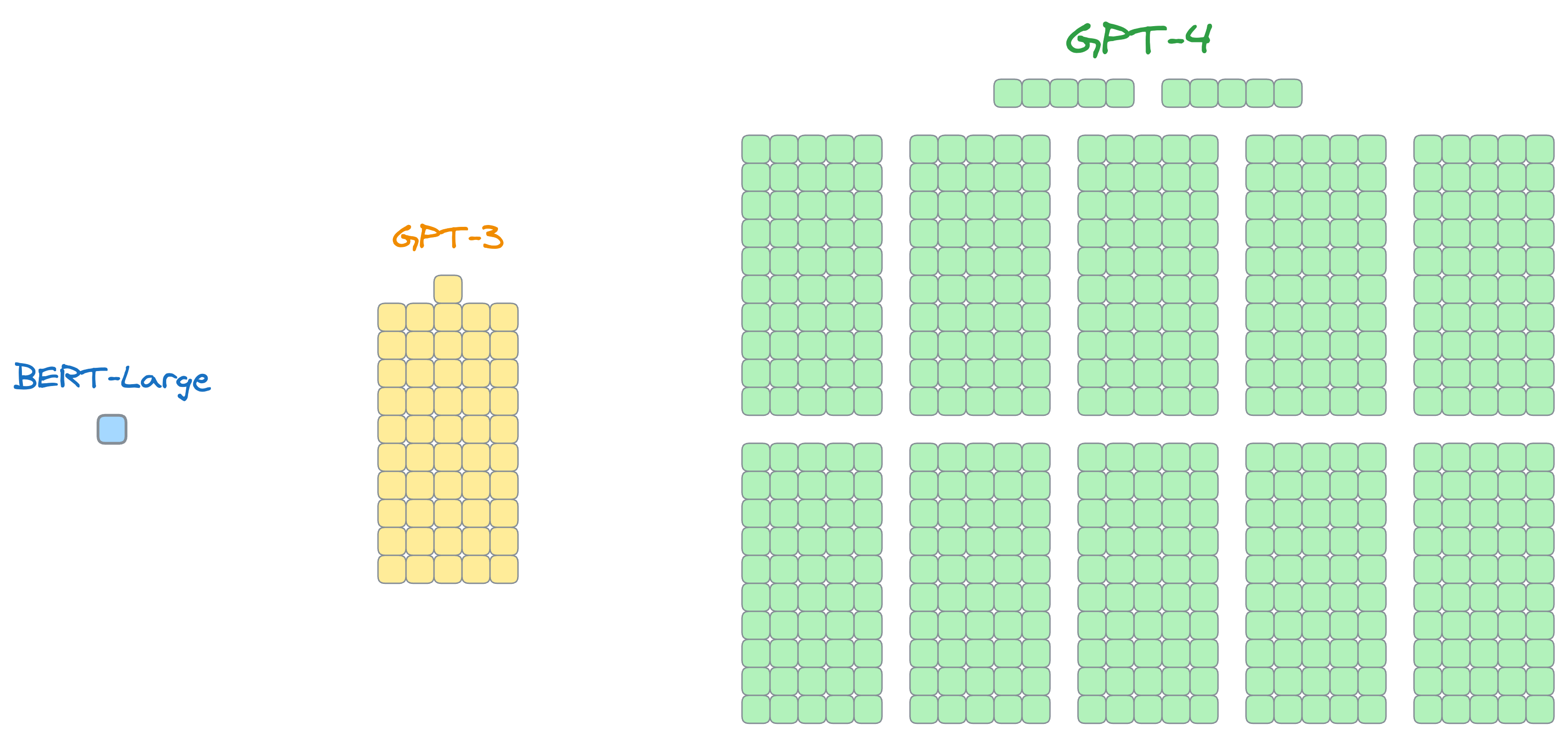
Traditional fine-tuning is just not practically feasible here, and in fact, not everyone can afford to do it due to a lack of massive infrastructure.
In fact, it’s not just about the availability of high computing power.
Consider this...
OpenAI trained GPT-3 and GPT-4 models in-house on massive GPU clusters, so they have access to them for sure.
However, they also provide a fine-tuning API to customize these models according to our application, which is currently available for the following models: gpt-3.5-turbo-1106, gpt-3.5-turbo-0613, babbage-002, davinci-002, and gpt-4-0613:
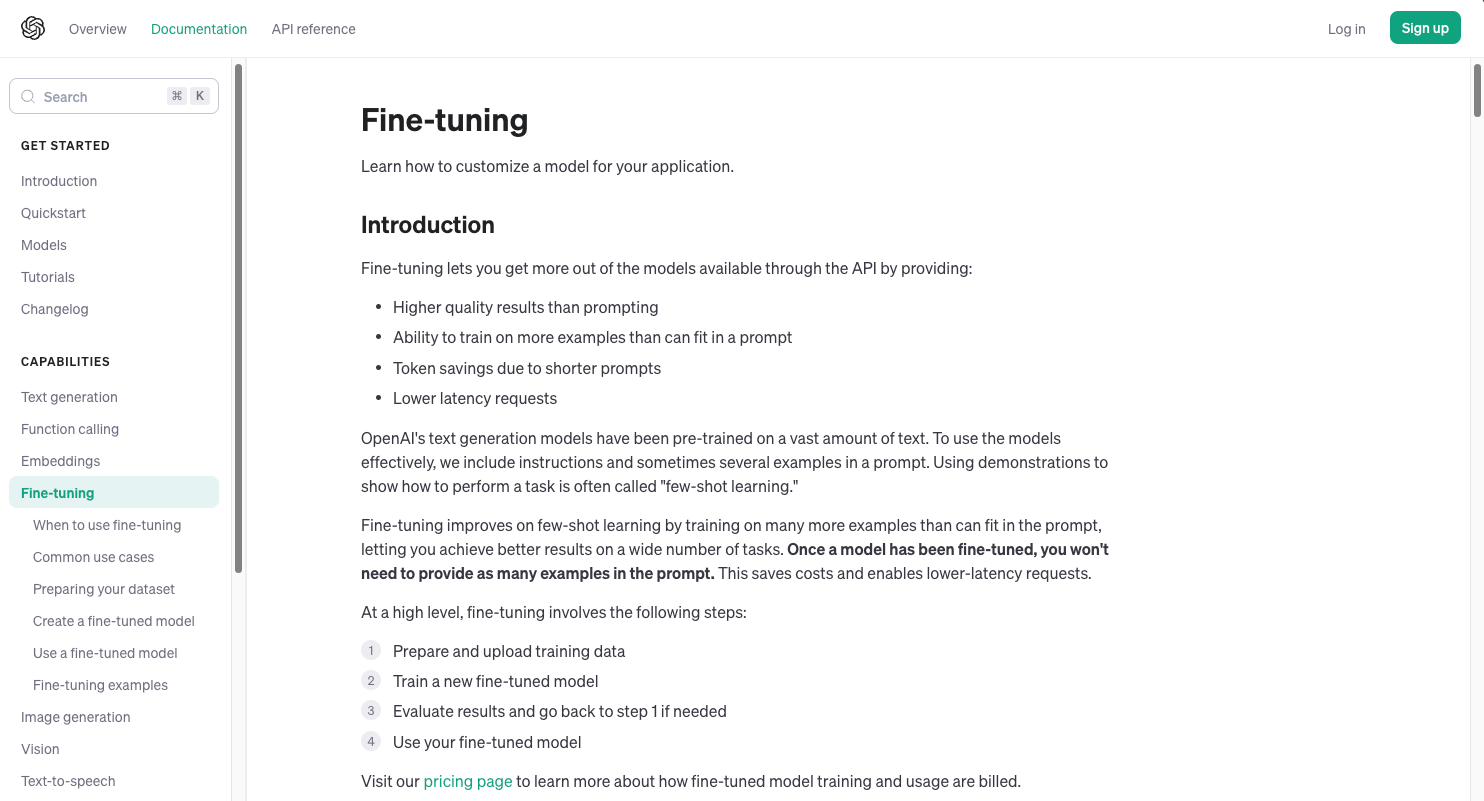
Going by traditional fine-tuning, for every customer wanting to have a customized version of any of these models, OpenAI would have to dedicate an entire GPU server to load it and also ensure that they maintain sufficient computing capabilities for fine-tuning requests.
Deploying such independent instances of fine-tuned models, each with 175B parameters, is prohibitively expensive.
To put it into perspective, a GPT-3 model checkpoint is estimated to consume about 350GBs. And this is the static memory of the model, which only includes model weights. It does not even consider the memory required during training, computing activations, running backpropagation, and more.
And to make things worse, what we discussed above is just for one customer, but they already have thousands of customers who create a customized version of OpenAI models that is fine-tuned to their dataset.
In fact, there are many other users who just want to explore the fine-tuning capabilities (for skill development or general exploration, maybe), but they may never want to use that model to serve any end-users.
This is crucial because OpenAI would still have to bear the cost of maintaining and serving the full fine-tuned model if even it receives no requests because they have implemented “Only pay for what you use” pricing strategy:
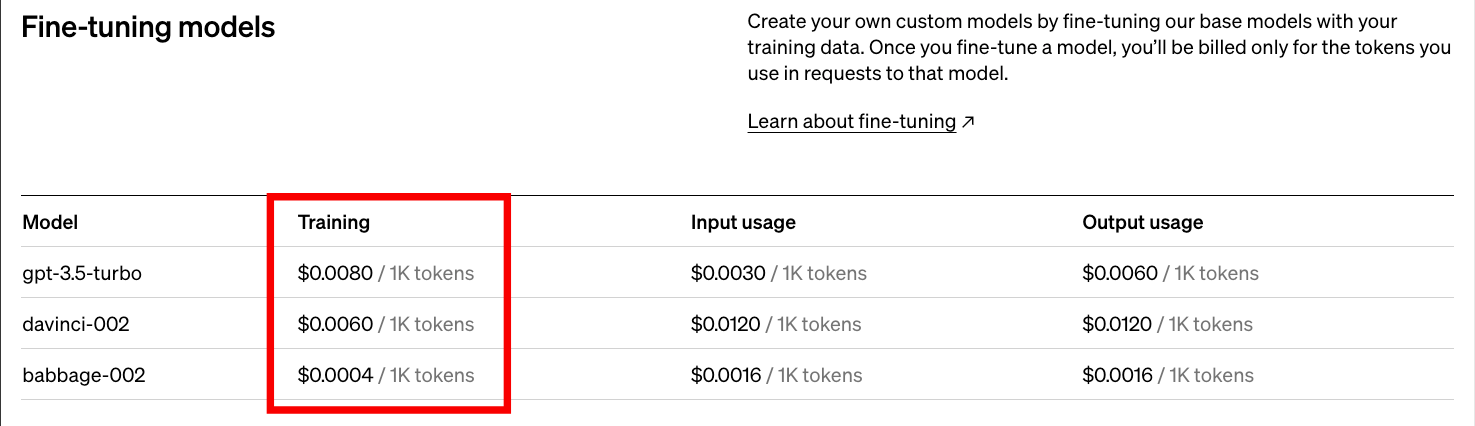
Thus, they never earn if the model is never used beyond fine-tuning, which is also not that expensive, as marked in the above image.
From the discussion so far, it must be clear that such scenarios pose a significant challenge for traditional fine-tuning approaches.
The computational resources and time required to fine-tune these large models for individual customers would be immense.
Additionally, maintaining the infrastructure to support fine-tuning requests from potentially thousands of customers simultaneously would be a huge task for them.
LoRA and QLoRA are two superb techniques to address this practical limitation.
Today, I will walk you through:
- What they are?
- How do they work?
- Why are they so effective?
- And how to implement them from Scratch in PyTorch?
Low-Rank Adaptation (LoRA)
The whole idea behind LoRA is pretty simple and smart.
In a gist, this technique allows us to efficiently fine-tune pre-trained neural networks. Yes, they don’t have to be LLMs necessarily as they can be used across a wide range of neural networks.
The core idea revolves around training very few parameters in comparison to the base model, say, full GPT-3, while preserving the performance that we would otherwise get with full-model fine-tuning (which we discussed above).
Let’s get into more detail in the upcoming sections.
Background
First, let us understand an inspiring observation that will help us formulate the LoRA in an upcoming section.
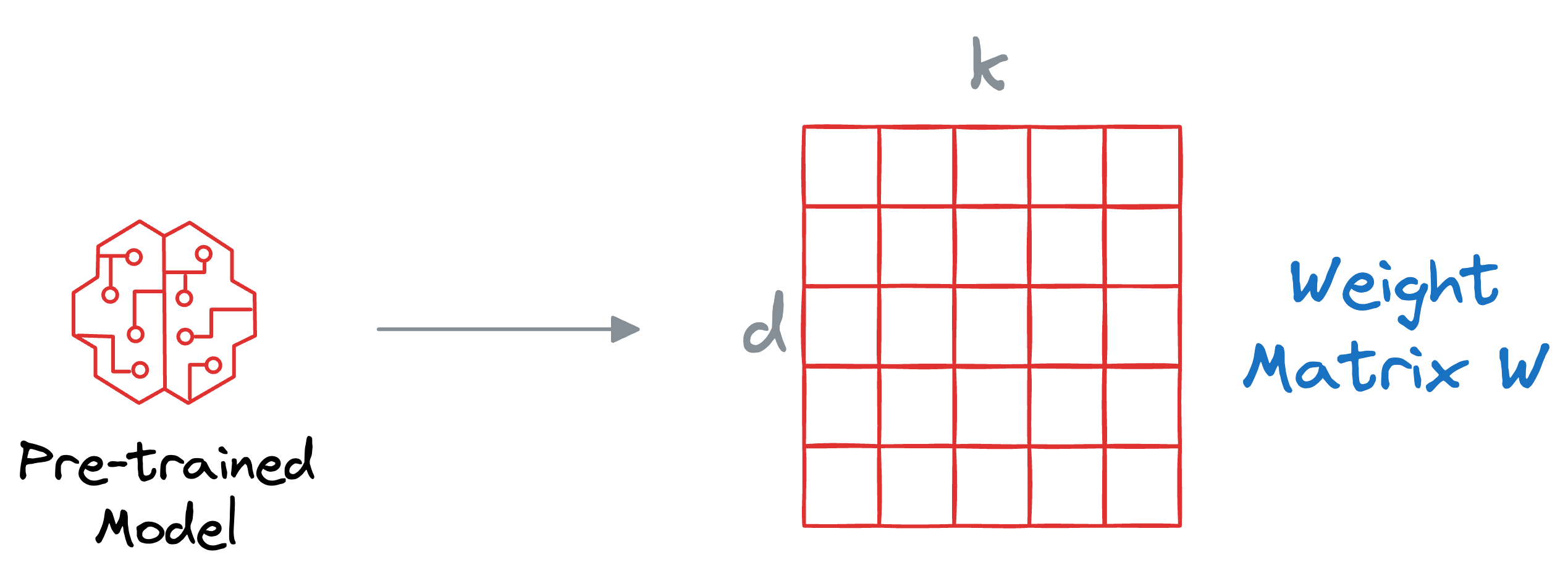
Consider the current weights of some random layer in the pre-trained model are $W$ of dimensions $d*k$, and we wish to fine-tune it on some other dataset.
During fine-tuning, the gradient update rule suggests that we must add $\Delta W$ to get the updated parameters:
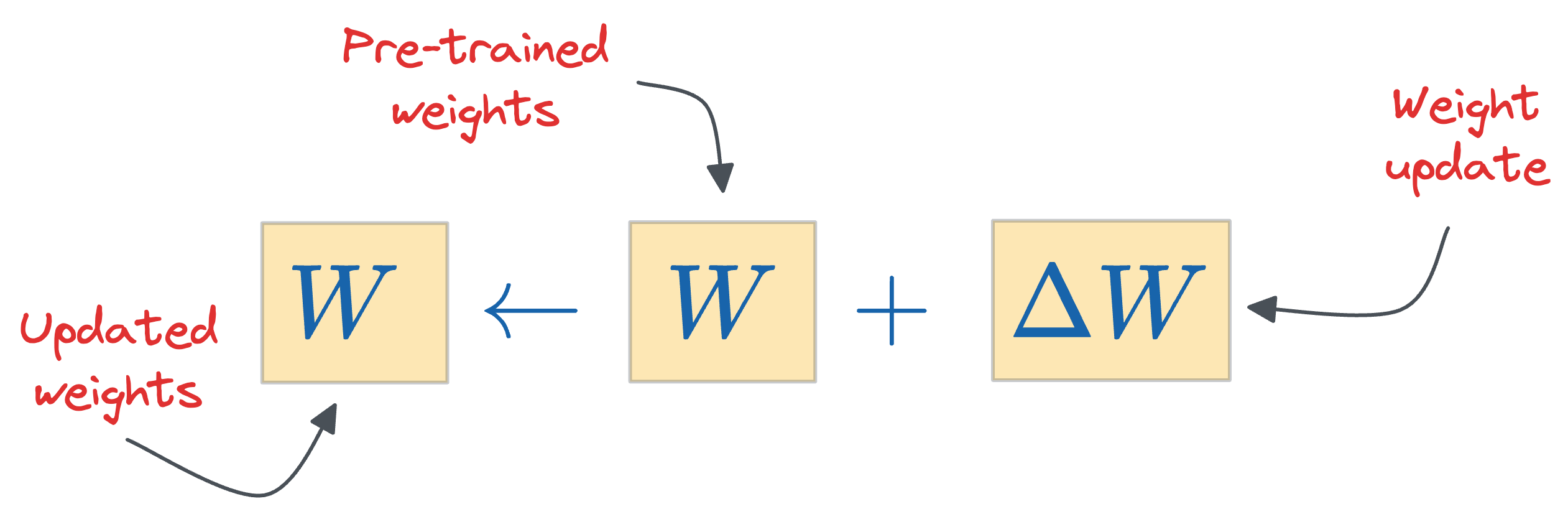
For simplicity, you can think about $\Delta W$ as the update obtained after running gradient descent on the new dataset:
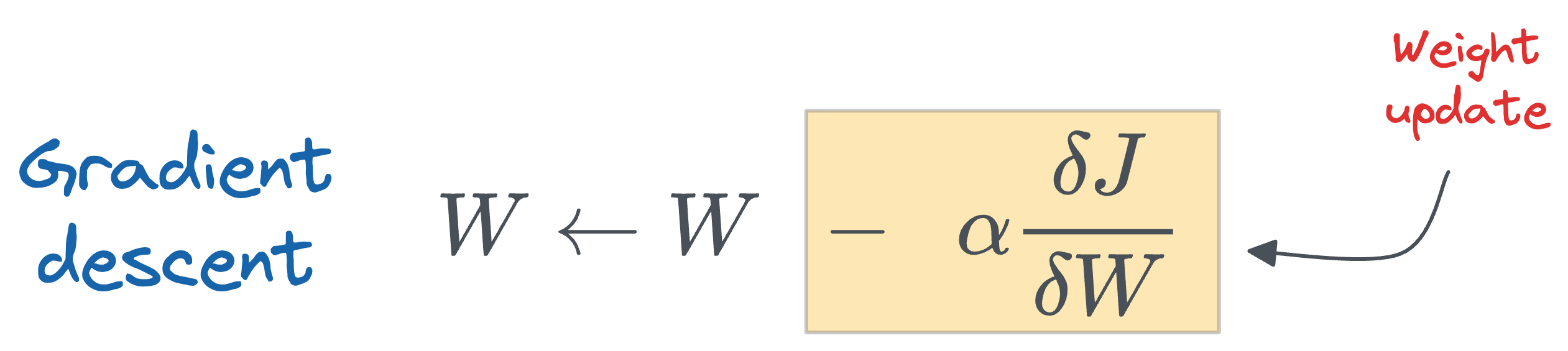
Also, instead of updating the original weights $W$, it is perfectly legal to maintain both matrics, $W$ and $\Delta W$.
During inference, we can compute the prediction on an input sample $x$ as follows:
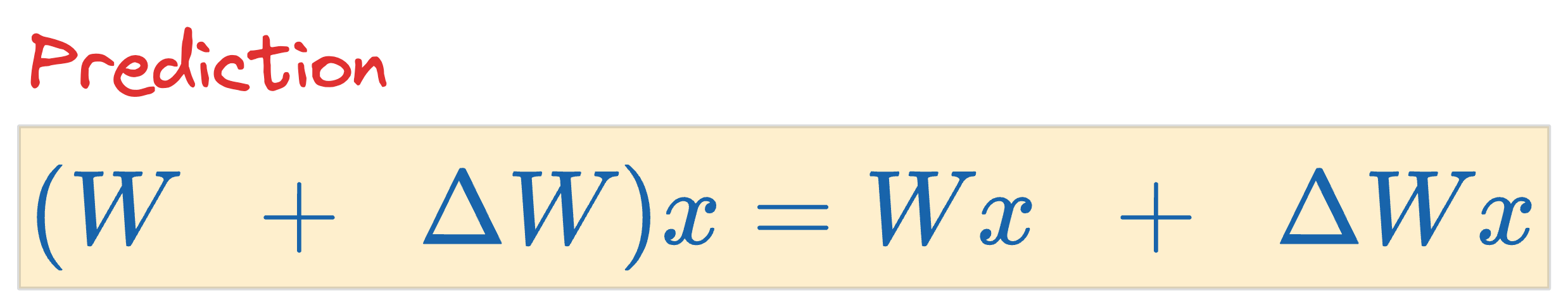
In fact, in all the model fine-tuning iterations, $W$ can be kept static, and all weight updates using gradient computation can be incorporated to $\Delta W$ instead.
But you might be wondering...how does that even help?
The matrix $W$ is already huge, and we are talking about introducing another matrix that is equally big.
So, we must introduce some smart tricks to manipulate $\Delta W$ so that we can fulfill the fine-tuning objective while ensuring we do not consume high memory.
Now, we really can’t do much about $W$ as these weights refer to the pre-trained model. So all optimization (if we intend to use any) must be done $\Delta W$ instead.
While doing so, we must also remember that currently, both $W$ and $\Delta W$ have the same dimensions.
But given that $W$ already is huge, we must ensure that $\Delta W$ does not end up being of the same dimensions, as this will defeat the entire purpose of efficient fine-tuning.
In other words, if we were to keep $\Delta W$ of the same dimensions as $W$, then it would have been better if we had fine-tuned the original model itself.
How LoRA works?
Now, you might be thinking...
But how can we even add two matrics if both have different dimensions?
It’s true, we can’t do that.
More specifically, during fine-tuning, the weight matrix $W$ is frozen, so it does not receive any gradient updates. Thus, all gradient updates are redirected to the $\Delta W$ matrix.
Read the full article
Sign up now to read the full article and get access to all articles for paying subscribers only.
Join today!




