Conformal Predictions: Build Confidence in Your ML Model's Predictions

The problem

Blindly trusting an ML model’s predictions can be fatal at times, especially in high-stakes environments where decisions based on these predictions can affect human lives, financial stability, or critical infrastructure.

While an accuracy of “95%” looks good on paper, the model will never tell you which specific 5% of its predictions are incorrect when used in downstream tasks.

To put it another way, although we may know that the model’s predictions are generally correct a certain percentage of the time, but the model typically cannot tell much about a specific prediction.

As a result, in high-risk situations like medical diagnostics, for instance, blindly trusting every prediction can result in severe health outcomes.

Similarly, in finance, even a single erroneous prediction could cause substantial monetary losses or misguided investment strategies.

Thus, to mitigate such risks, it is essential to not only solely rely on the predictions but also understand and quantify the uncertainty associated with these predictions.

If we don't have any way to understand the model's confidence, then an accurate prediction and a guess can look the same.

Let's build some more motivation around this idea and why we need prediction intervals for models like neural networks.

To begin, we know these models are likely going to be used in downstream decision-making tasks.

For instance, if you are a doctor and you get this MRI along, an output from the model that suggests that the person is normal and doesn't need any treatment is likely pretty unuseful to you.

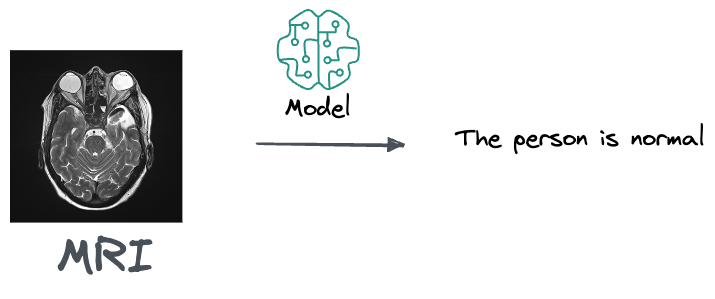
This is because a doctor's job is to do a differential diagnosis. Thus, what they really care about is knowing if there's a 10% percent chance that that person has cancer, based on that MRI.

Another thing that will be more useful is getting a prediction set, which is a set of diagnoses that are guaranteed with high probability.

For instance, this prediction set could indicate that there's a 90% probability that the true diagnosis is contained within the prediction set.

If this is the output, the doctor can use that in the process and rule out diagnoses.

The solution

Conformal prediction, also known as conformal inference, provides a framework for generating prediction intervals or sets that come with strong statistical guarantees.

What sets conformal prediction apart is its distribution-free nature, meaning it does not rely on any assumptions about the underlying data distribution or the specific model used.

Moreover, it requires no additional training. The whole model can be a black box and still be used to make conformal predictions.

Due to its nature, integrating conformal prediction with any pre-trained machine learning model allows practitioners to transform single-point predictions into intervals or sets that are (almost) guaranteed to contain the true outcome with a user-specified probability.

For example, in a classification task like medical diagnosis, the traditional approach would output a single class label. This single-point prediction leaves no room for understanding the confidence in the prediction or for considering other plausible diagnoses.

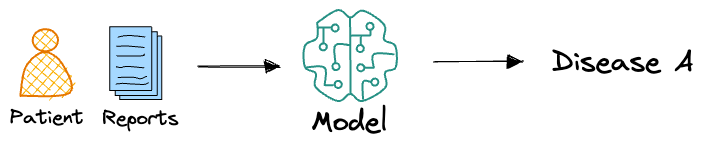
In contrast, a conformal prediction approach would generate a set of possible diagnoses, ensuring that the true diagnosis is included within this set with a specified confidence level, such as 95%.

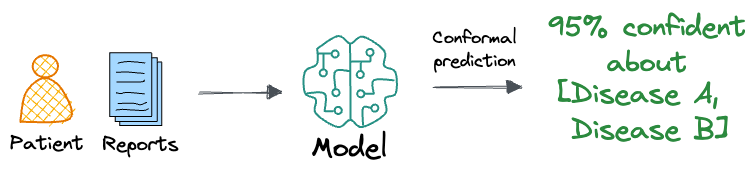
For instance, instead of merely predicting "disease A" with 95% probability, a conformal predictor might output a set that includes "disease A" and "disease B," guaranteeing that the correct diagnosis lies within this set 95% of the time.

It's okay if nothing is clear to you yet since we will understand this in detail in the next section.

More specifically, in the following sections:

• We will explore the theoretical foundations of conformal prediction, detailing how it achieves its distribution-free guarantees and why it is effective in uncertainty quantification.
• We will also dive into practical applications, demonstrating how to implement conformal prediction in various machine learning tasks, like classification.

Let's begin!

Conformal Prediction

Imagine we have a dataset, say, images, and there are multiple labels (a total of $K$) in this dataset:

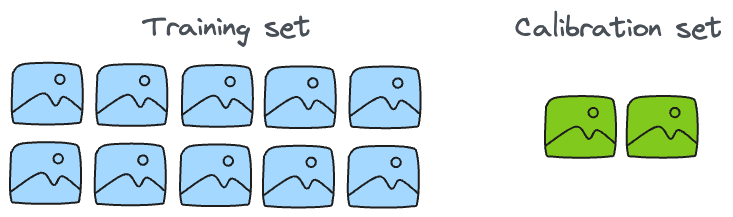
In conformal predictions, a new set, called the "calibration set" is extracted from the training data. It does not have to be super large. For instance, in the case of a dataset of 60k images, it would be okay to separate out just 500-750 images as the calibration set:

To keep things simple, also imagine that we have already trained a model on the above training dataset, say, a neural network:

Mathematically, this model can be denoted as follows:

• $f_y​(x)$ denotes the model's predicted probability that the target variable $Y$ takes on the value $y$ ($y$ can be any value from the above class labels) on a specific input $X=x$.
• $P[Y=y | X=x]$ represents the true conditional probability of $Y=y$ given $X=x$.

So, $f_y​(x)$ is the model's approximation of the true underlying conditional probability $P[Y=y | X=x]$. The goal of the model is to accurately estimate this probability, enabling reliable predictions and uncertainty quantification.

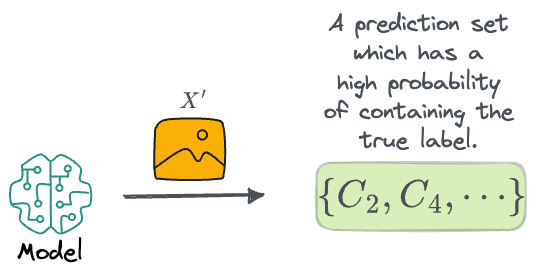
Once the model has been trained, our goal is to take any new example $X'$ (say the model is being used in a downstream application, so the label is unknown) and generate a prediction set $\phi(X')$ such that it is expected to contain the true class $Y'$ with a high probability.