Introduction
Hyperparameter tuning is a tedious and time-consuming task in training machine learning (ML) models.
Typically, the most common way to determine the optimal set of hyperparameters is through repeated experimentation.
Essentially, we define a set of hyperparameter configurations (mainly through random guessing) and run them through our model. Finally, we choose the model which returns the most optimal performance metric.
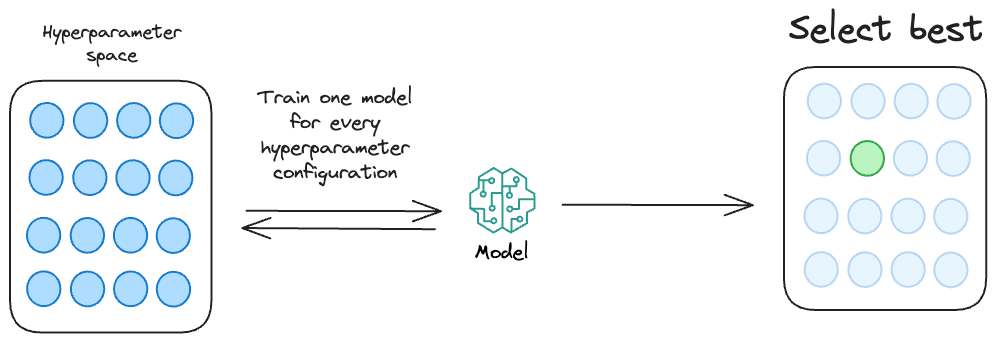
This is called hyperparameter tuning.
While this approach is feasible for training small-scale ML models, it is practically infeasible when training bigger models.
To get some perspective, imagine if it takes $1.5$ hours to train a model and you have set $20$ different hyperparameter configurations to run through your model.
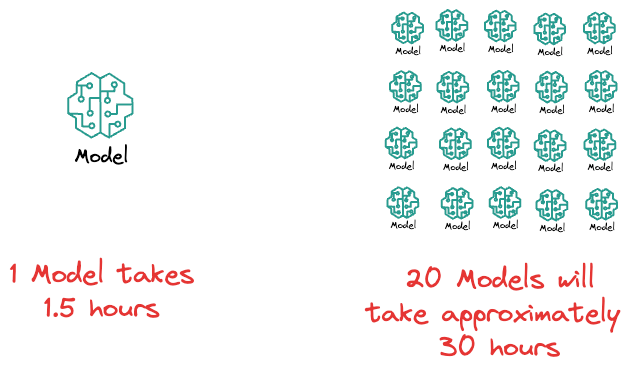
That's more than a day of training.
Therefore, learning about optimized hyperparameter tuning strategies and utilizing them is extremely important to build large ML models.
Bayesian optimization is a highly underappreciated yet immensely powerful approach for tuning hyperparameters.
It revolves around the idea of using Bayesian statistics to estimate the distribution of the best hyperparameters for a model.
While iterating over different hyperparameter configurations, the Bayesian optimization algorithm constantly updates its beliefs about the distribution of hyperparameters by observing model performance corresponding to each hyperparameter.
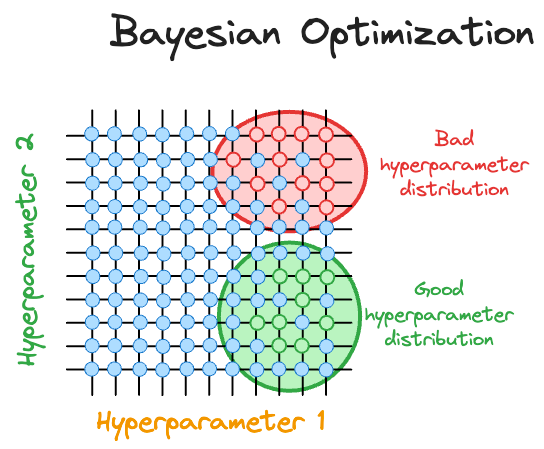
This allows it to take informed steps to select the next set of hyperparameters, gradually converging to an optimal set of hyperparameters.
Thus, in this blog, let's explore how Bayesian optimization works and why it is so powerful.
More specifically, we shall cover:
- Issues with traditional hyperparameter tuning approaches.
- What is the motivation for Bayesian optimization?
- How does Bayesian optimization work?
- The intuition behind Bayesian optimization.
- Results from the research paper which proposed Bayesian optimization for hyperparameter tuning.
- A hands-on Bayesian optimization experiment.
- Comparing Bayesian optimization with grid search and random search.
- Analyzing the results of Bayesian optimization.
- Best practices for using Bayesian optimization.
Let's begin!
Issues with traditional approaches
Before understanding the importance of using faster tuning strategies, it is essential to understand the problems with existing techniques.
The three most common methods of hyperparameter tuning are:
#1) Manual search: This involves human intuition and expertise to manually adjust hyperparameters based on domain knowledge and trial-and-error.
#2) Grid search: Grid search explores all possible combinations of hyperparameters specified with a range.
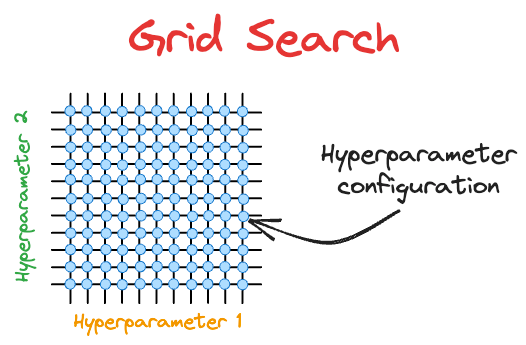
#3) Random search: Random search is similar to grid search, but instead of searching all configurations specified in grid search, it tests only randomly selected configurations.
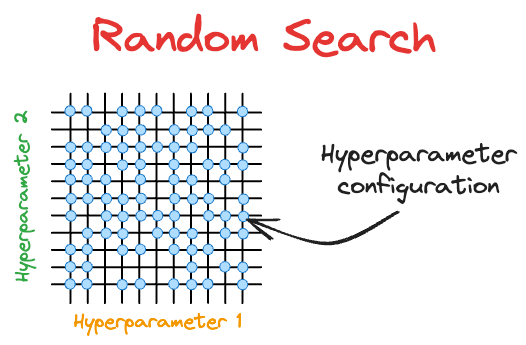
Issue #1) Computational complexity
It is practically infeasible to train a model (especially those that take plenty of time) for every possible combination of hyperparameters with grid search.
For instance, if there are N different hyperparameters $(H_{1}, H_{2}, \cdots, H_{N})$, each with $(K_{1}, K_{2}, \cdots, K_{N})$ prespecified values, total number of models become:
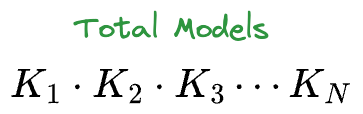
Issue #2) Limited search space
In both techniques, we specify a desired range of hyperparameter values to search over.
Yet, the ideal hyperparameter may exist outside that range.
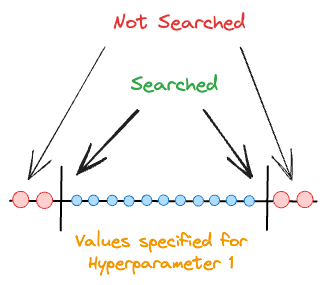
This inherently introduces some bias in hyperparameter tuning.
Also, expanding the hyperparameter search space will drastically increase the overall run time.
Issue #3) Limited to discrete search space
Hyperparameters can be categorized into two categories based on the values they can take:
- Continuous: learning rate, regularization rate, dropout rate, etc.
- Discrete: Batch size, kernel type in support vector machines (SVMs), etc.
Yet, for continuous hyperparameters, we can only set discrete values in grid search and random search.
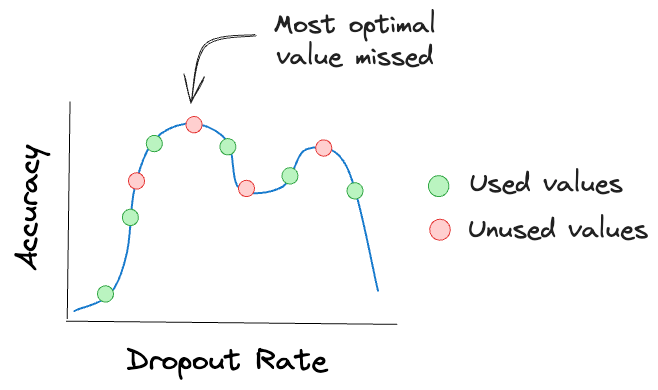
Thus, it is possible that we may miss the optimal value for a continuous hyperparameter, as illustrated in the image above.
Bayesian hyperparameter optimization
By now, we are convinced that traditional hyperparameter tuning techniques have numerous limitations.
Motivation for Bayesian optimization
Essentially, it's obvious to understand that the primary objective of hyperparameter tuning is to find a specific set of hyperparameters that optimize some score function.
Considering the score function $(f)$ to be an error function, we can express hyperparameter search as follows:
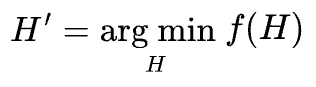
The objective is to minimize the error function $f$ for all possible values of hyperparameter $H$.
However, another problem with traditional methods like grid search (or random search) is that each hyperparameter trial is independent of other trials.
In other words, they do not consider the previous results to select the subsequent hyperparameters.
As a result, they are entirely uninformed by past evaluations and spend a significant amount of time evaluating “ideally non-optimal hyperparameters.”
For instance, consider the grid search diagram we discussed earlier.
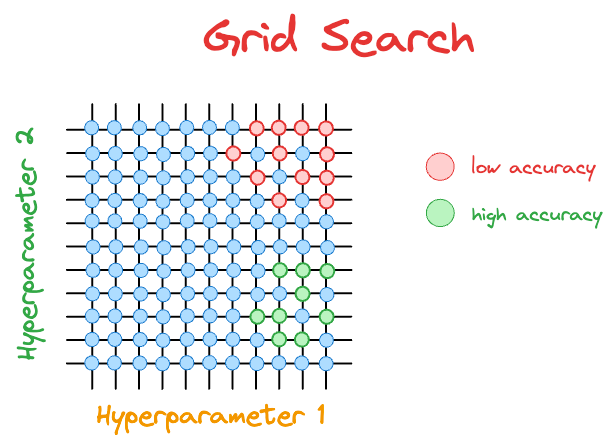
The hyperparameter configurations with low accuracy are marked in red, and those with high accuracy are marked in green.
After the $21$ model runs ($9$ green and $12$ red) depicted above, grid search will not make any informed guesses on which hyperparameter it should evaluate next.
