Introduction
We covered several details about graph learning with graph neural networks in the first part of this crash course.
While the first part was mainly an extensive introduction, I mentioned towards the end that we would get into more details and cover many of the advancements in graph learning in another article.
Thus, in this second part, we shall understand some of the limitations of the GNN architecture discussed in Part 1 and how they can be improved.
Everywhere, we have practical demos so that you can understand how these ideas are implemented in practice.
Let's begin with a quick recap first!
Recap
Feel free to skip to the next section if you remember what we discussed in Part 1.
Why graph learning?
Traditional deep learning typically relies on data formats that are tabular, image-based, or sequential (like language) in nature. These formats are well-suited for conventional neural network architectures like RNNs, CNNs, Transformers, etc.
These types of data are well-understood, and the models designed to handle them have become highly optimized.
However, with time, we have also realized the inherent challenges of such traditional approaches, one of which is their inability to naturally model complex relationships and dependencies between entities that are not easily captured by fixed grids or sequences.

More specifically, a significant proportion of our real-world data often exists in the form of graphs, where entities (nodes) are connected by relationships (edges), and these connections carry significant meaning, which, if we knew how to model, can lead to much more robust models.
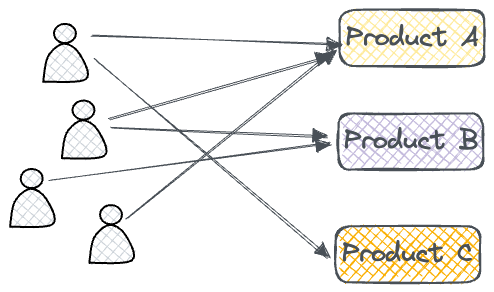
For instance, instead of representing e-commerce data in a tabular form (this user purchased this product at this time for this amount...), it can be better represented as interactions between users and products in the form of graphs. As a result, we can use this representation to learn from and possibly make more relevant personalized recommendations.
The field of Graph Neural Networks (GNNs) intends to fill this gap, offering a way to extend deep learning techniques to graph-structured data. As a result, they have been emerging as a technique to learn smartly from data.
Several research papers have proven that they can lead to more accurate and robust models, and such models are being actively used in real-world systems.
This is due to their ability to learn sophisticated representations (embeddings) using the graph structure and combining it with the predictive power of deep learning models we use today.
Challenges
But given the unique characteristics of graph data, they do not naturally fit into the traditional deep learning models and pose several modeling challenges that we need to be aware of.
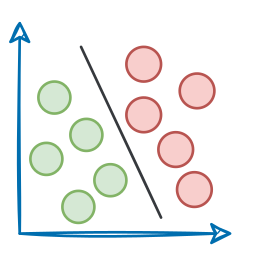
1) Irregular shapes
Unlike images or sequences, graphs are highly irregular.
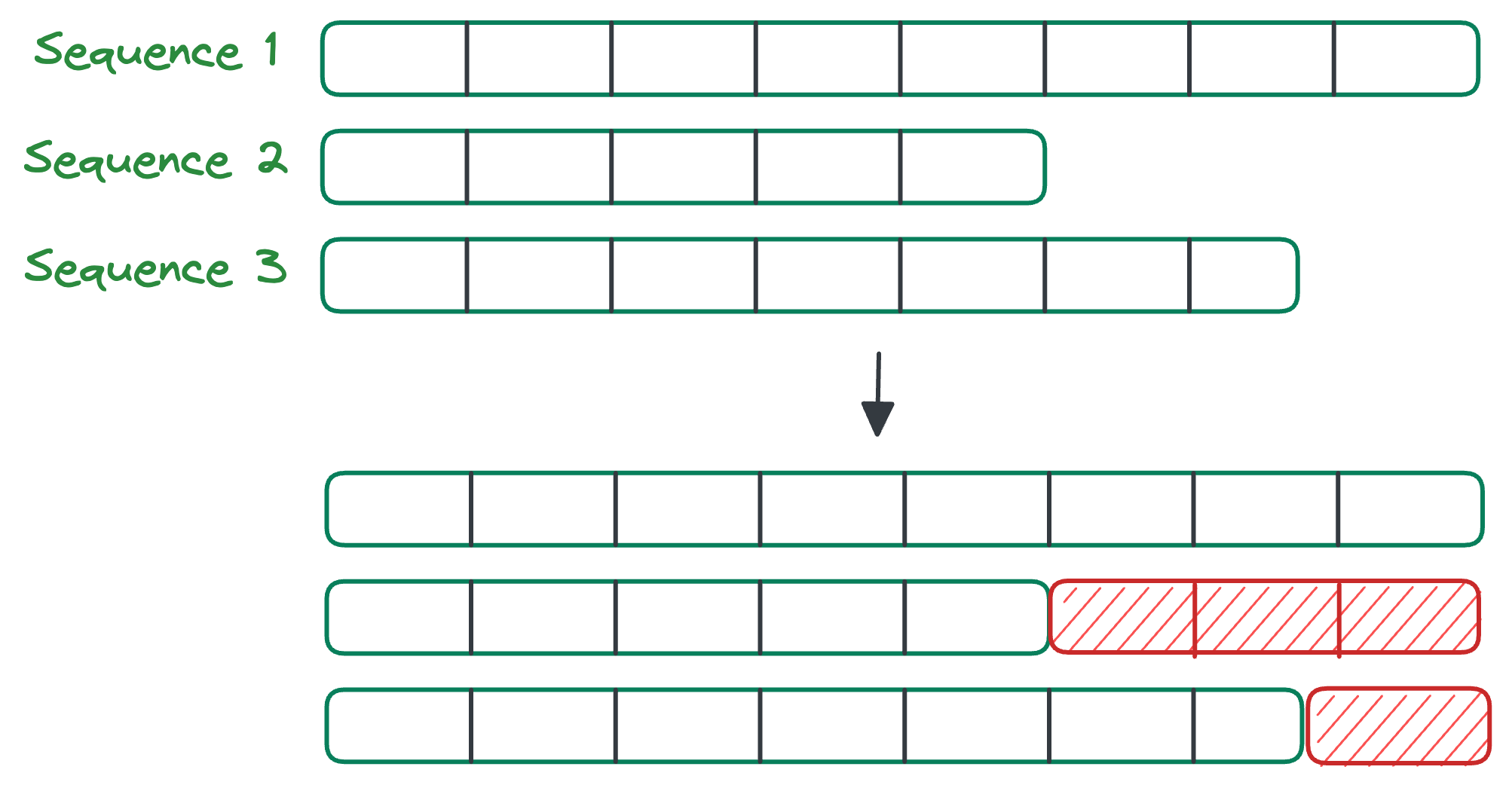
Images and sequences can be irregular though. But we have ways to address this. For instance, in case of sequence modeling, you would typically pad the sequences to match the maximum sequence length:
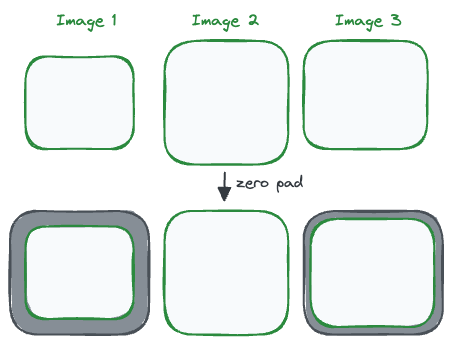
Similarly, in case of images, we would pad the images or center crop them to make them of equal size and width:
Graphs are different.
They can vary widely in the number of nodes, and each node can have a different number of neighbors.
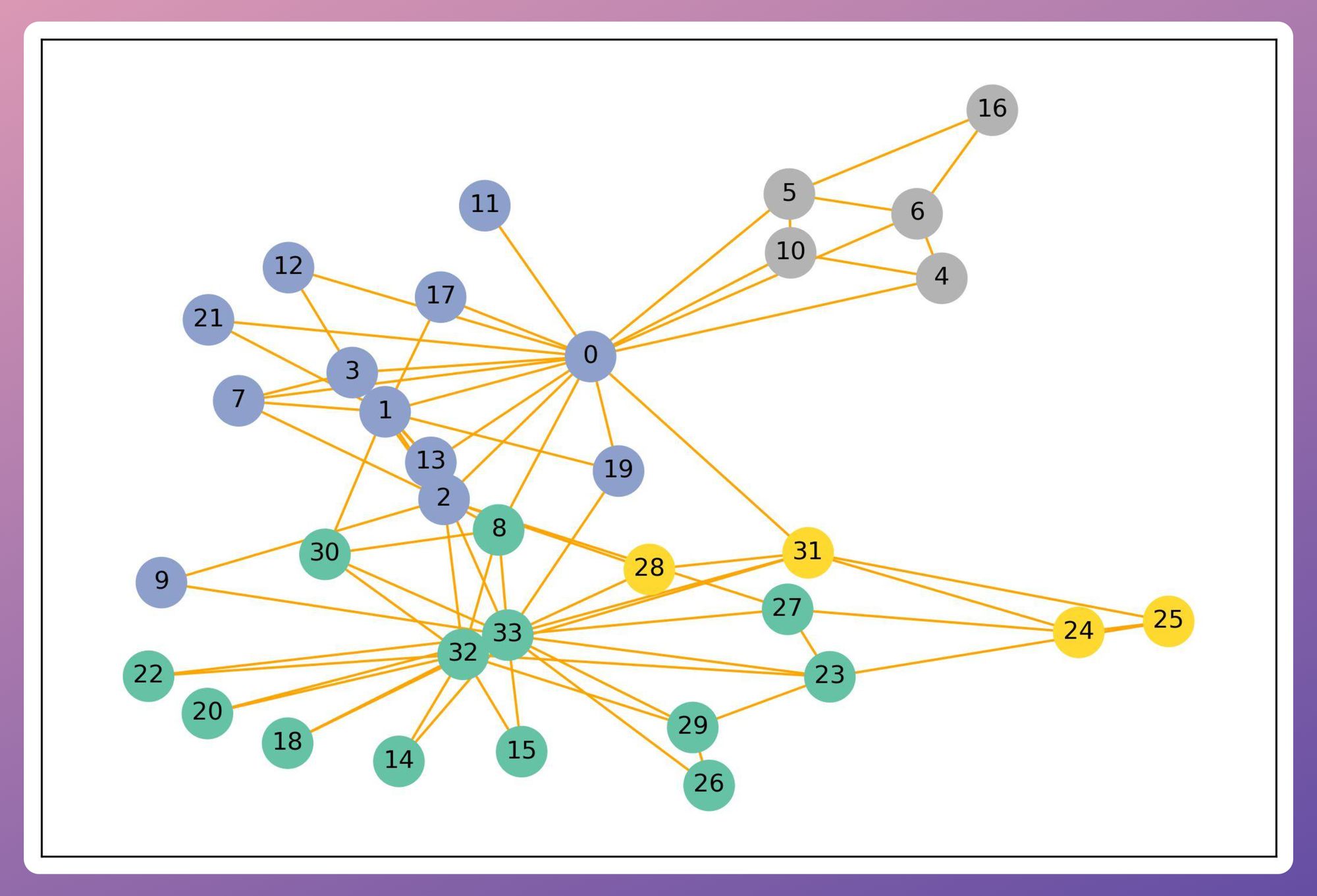
This irregular structure complicates the design of neural operations that are straightforward in other domains, such as convolution or pooling, which rely on consistent input shapes and sizes.
2) Interdependence of data points
Typical machine learning models often assume that instances in the dataset are independent of one another.
However, in graph data, this assumption doesn't hold because each node is inherently connected to others through various types of relationships, such as citations, friendships, or interactions.
The interconnected nature of graph data requires models that can account for these dependencies, which conventional models are not designed to handle.
3) Permutation invariance
In traditional data formats like images and text, the order or structure of the data is fixed and meaningful.
For example, in an image, the spatial arrangement of pixels is crucial; a convolutional neural network (CNN) processes an image by scanning through pixels in a specific order, typically left-to-right, top-to-bottom.
Similarly, in text data, the sequence of words is essential for understanding context, so recurrent neural networks (RNNs) process the data in a fixed order. Changing the order of words will change the meaning of the sentence and modeling results.

Graph data, yet again, is fundamentally different.
In a graph, nodes (representing entities) are connected by edges (representing relationships), and there is no inherent ordering of these nodes. This lack of a natural order is what we refer to as "permutation invariance."
Thus, when working with graph data, the model should produce the same output regardless of the order in which the nodes and their neighbors are presented.
For instance, consider a social network where each person (node) is connected to others (neighbors).
Whether you list Alice’s connections as [Bob, Carol, Dave] or [Dave, Bob, Carol] should not change the prediction or outcome related to Alice. The model must treat these permutations of the input as equivalent.
Graph Convolutional Networks (GCNs)
Graph Convolutional Networks (GCNs) stand out as the most widely applied architecture for graph learning.
The idea is quite similar to how the traditional convolution neural networks for.
- Recall that CNNs aggregate feature information from spatially defined patches in an image using the convolution operations:

- GCNs work in a similar manner, wherein, they try to aggregate information based on local graph neighborhoods:
We covered the technical details in the first part, so we won't cover them again:

But the hidden state for a particular node was defined in a form similar to the one below:
Read the full article
Sign up now to read the full article and get access to all articles for paying subscribers only.
Join today!