The problem
The neural network architectures we are building today are undoubtedly much more accurate than they have ever been in their entire history.
However, many experiments have revealed that modern neural networks are no longer well-calibrated.
Simply put, a model is perfectly calibrated if the predicted probabilities of outcomes align closely with the actual outcomes. If a model predicts an event with a 70% probability, then ideally, out of 100 such predictions, approximately 70 should result in the event occurring.
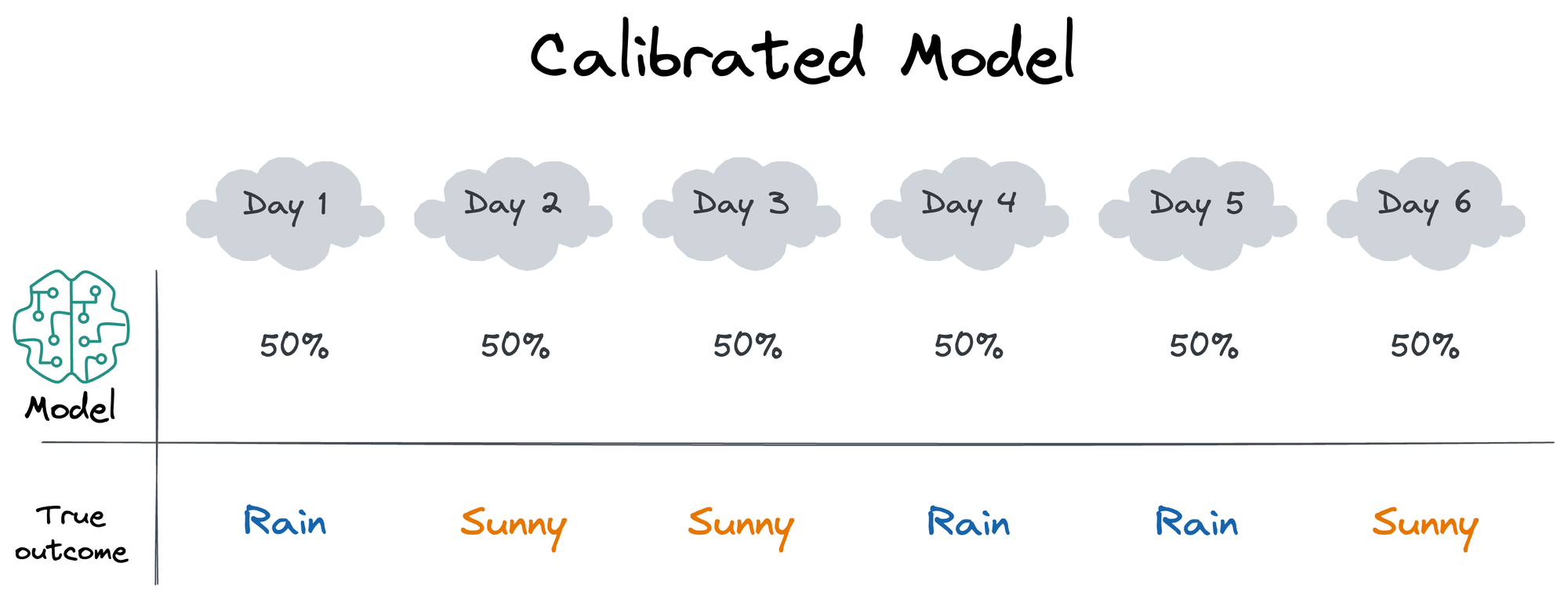
For instance, assume that over many days (could be consecutive or non-consecutive), the model predicted a 50% chance of rain. To measure if these predictions are well calibrated, you would calculate how often it actually rains.
If, over the long run, it really did rain about 50% of the time, it means the model's prediction (or forecasts) were well calibrated. However, if it rained just 25%, or, say, 70% percent of the time, the model wasn't calibrated.
While calibration seems like a straightforward and perhaps trivial property that all networks must implicitly possess, many studies have shown that modern neural networks appear to lose this ability, and as a result, they tend to be overly confident in their predictions.
For instance, consider the following plot, which compares a LeNet (developed in 1998) with a ResNet (developed in 2016) on the CIFAR-100 dataset.
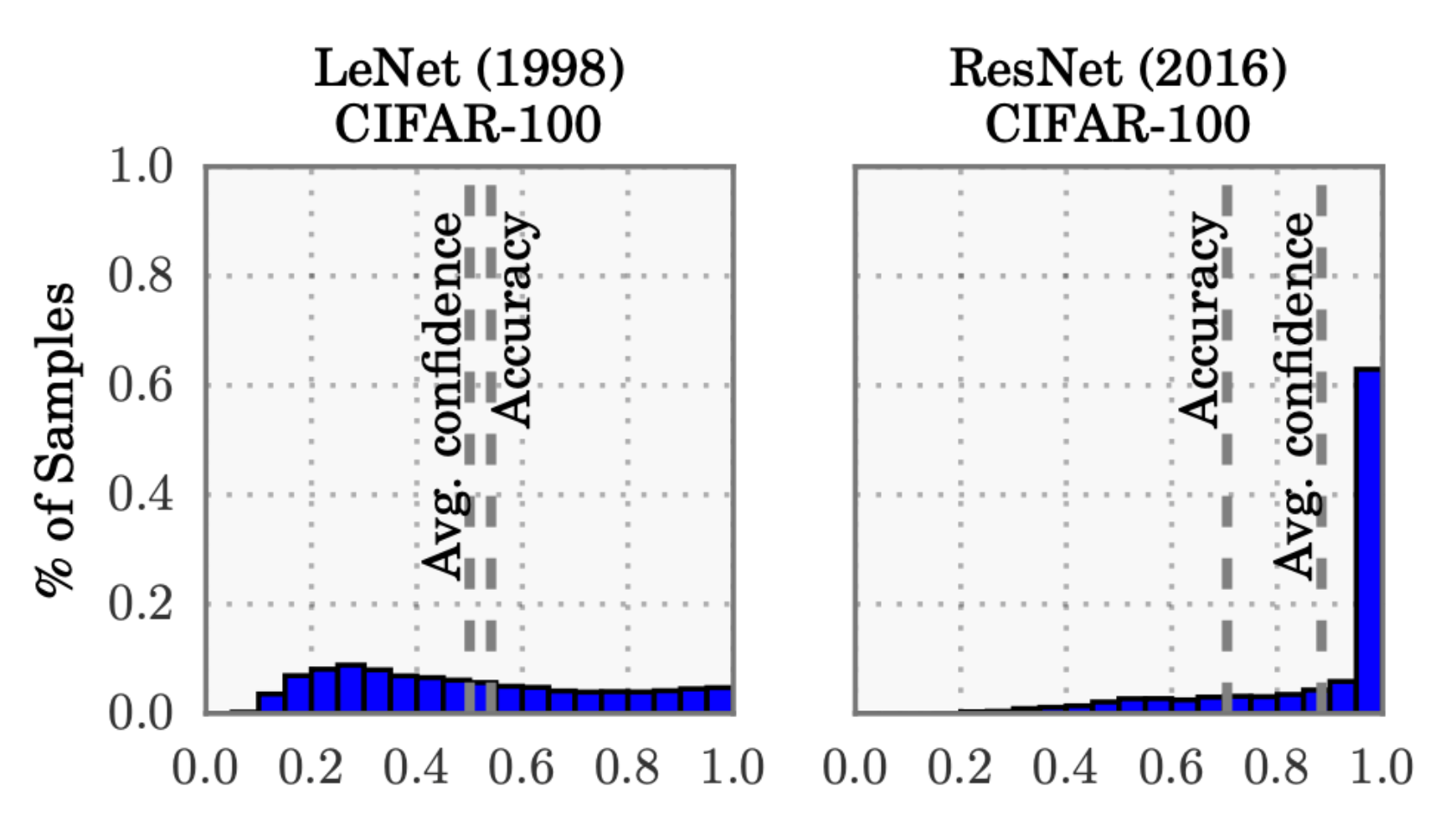
From the above plot, it is clear that:
- The average confidence of LeNet (an old model) closely matches its accuracy.
- In contrast, the average confidence of the ResNet (a relatively modern model) is substantially higher than its accuracy.
Thus, we can see that the LeNet model is well-calibrated since its confidence closely matches the expected accuracy. However, the ResNet’s accuracy is better ($0.7 \gt 0.5$), but the accuracy does not match its confidence.
To put it another way, it means that the ResNet model, despite being more accurate overall, is overconfident in its predictions. So, while LeNet's average confidence aligns well with its actual performance, indicating good calibration, ResNet's higher average confidence compared to its accuracy shows that it often predicts outcomes with higher certainty than warranted.
Why calibration is important?
One question that typically comes up at this stage is:
Why do we care about calibrating models, especially when we are able to build more accurate systems?
The motivation is quite similar to what we also discussed in the conformal prediction deep dive linked below:

Blindly trusting an ML model’s predictions can be fatal at times, especially in high-stakes environments where decisions based on these predictions can affect human lives, financial stability, or critical infrastructure.
While an accuracy of “95%” looks good on paper, the model will never tell you which specific 5% of its predictions are incorrect when used in downstream tasks.
To put it another way, although we may know that the model’s predictions are generally correct a certain percentage of the time, the model typically cannot tell much about a specific prediction.
As a result, in high-risk situations like medical diagnostics, for instance, blindly trusting every prediction can result in severe health outcomes.
Thus, to mitigate such risks, it is essential to not only solely rely on the predictions but also understand and quantify the uncertainty associated with these predictions.

But given that modern models are turning out to be overly confident in their predictions (which we also saw above), it is important to ensure that our model isn't one of them.
Such overconfidence can be problematic, especially in applications where the predicted probabilities are used to make critical decisions.
For instance, consider automated medical diagnostics once again. In such cases, control should be passed on to human doctors when the model's confidence of a disease diagnosis network is low.
More specifically, a network should provide a calibrated confidence measure in addition to its prediction. In other words, the probability associated with the predicted class label should reflect its ground truth correctness likelihood.
And this is not just about communicating the true confidence. Calibrated confidence estimates are also crucial for model interpretability.
Humans have a natural cognitive intuition towards probabilities. Good confidence estimates provide a valuable extra bit of information to establish trustworthiness with the user – especially for neural networks, whose classification decisions are often difficult to interpret.
But if we don't have any way to truly understand the model's confidence, then an accurate prediction and a guess can look the same.
Lastly, in many complex machine learning systems, models depend on each other and can also interact with each other. Single classifiers are often inputs into larger systems that make the final decisions.
If the models are calibrated, it simplifies interaction. Calibration allows each model to focus on estimating its particular probabilities as well as possible. And since the interpretation is stable, other system components don’t need to shift whenever models change.
On a side note, model calibration can work on a conditional level too. For instance, in the earlier example of rain forecast, we only measured calibration based on the model's predicted probability and if that probability was sustained over the long run in real life. This is depicted below:

However, a calibrated model could involve conditional probabilities as well.
In other words, while the above model individually predicted the rain on a particular day, it is wise to expect that the probability of rain is typically higher if it rained the previous day too.
Thus, a model that considers rain on the previous day and predicts $Pr(\text{Rain}|\text{Rained_Previous_Day} = 1)=0.7$ and $Pr(\text{Rain}|\text{Rained_Previous_Day} = 0)=0.3$ can be perfectly calibrated model and more useful too, provided these probabilities resonate with the actual outcomes.
Coming back to the topic...
The objective of this two-part crash course is two-fold:
- Understanding why neural networks in this era have become more miscalibrated than those produced years ago.
- I was formulating the true idea of model miscalibration.
- Defining techniques to measure the extent of miscalibration.
- Learning about methods that can help us reduce/eliminate miscalibration.
- And more.
In addition to this, we shall also discuss some insights and intuition into network training techniques and architectures that may cause miscalibration.
Defining calibration
First and foremost, let's define calibration in simple mathematical terms.
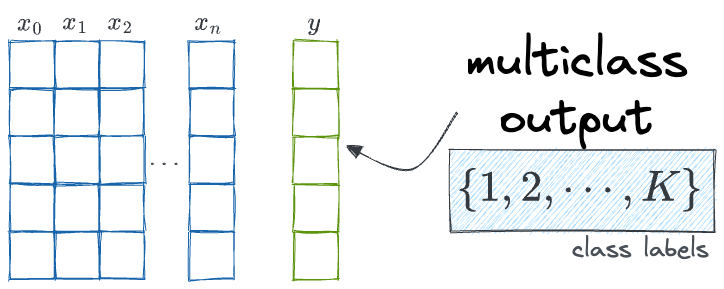
To begin, we are considering a supervised multiclass classification task:
This is modeled using a neural network that produces the probability of correctness of output (not true probabilities but ones estimated by the model):
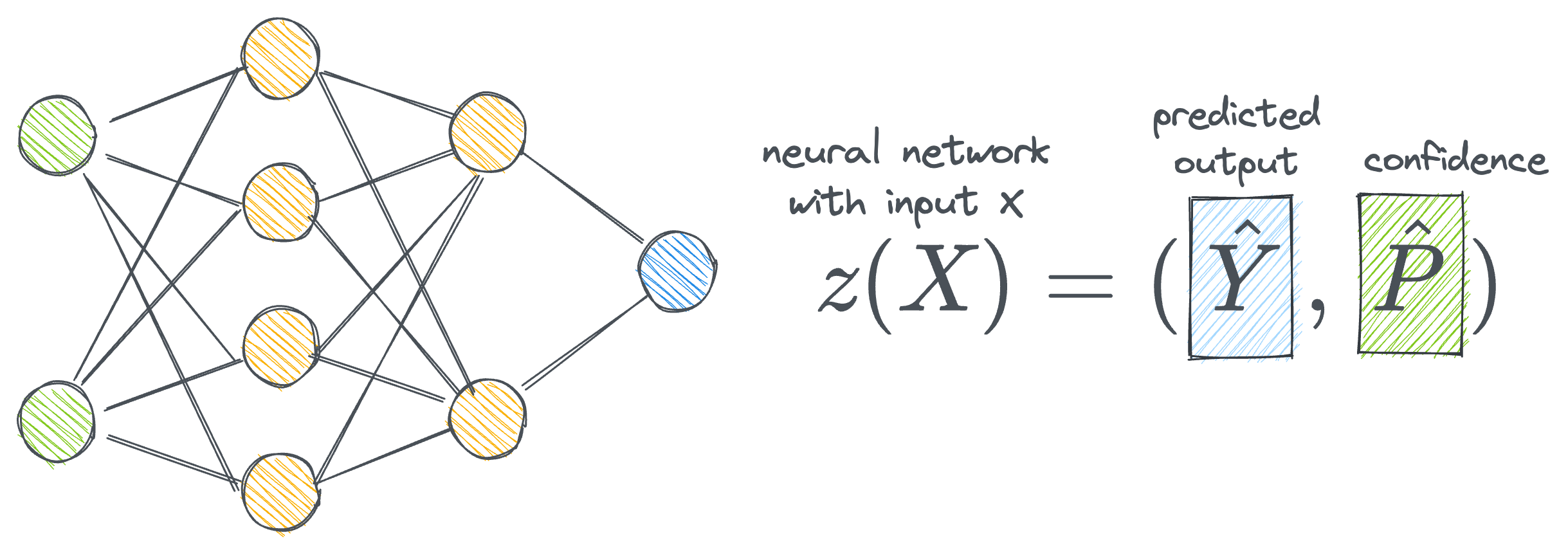
- $\hat Y$ is the predicted class.
- $\hat P$ is the corresponding confidence (through the softmax function).
The goal, as discussed earlier, is to ensure that the confidence estimate $\hat P$ is calibrated, which means that $\hat P$ represents a true probability of the event.
In other words, if the model predicted $\hat P=0.75$ on $100$ predictions, then it is expected that ~$75$ of those predictions are correctly classified.
Thus, we can define perfect calibration as follows:
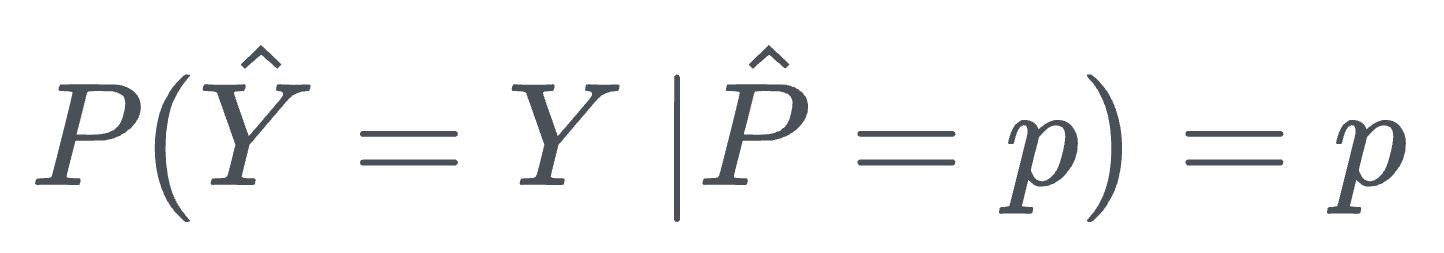
This definition means that for a perfectly calibrated model, the probability that the predicted label $\hat Y$ matches the true label $Y$, given that the model's predicted probability is $p$, should be exactly $p$.
In other words, the predicted probability $p$ should correspond directly to the actual frequency of correct predictions. If the model predicts a 75% chance of an event, it should indeed occur 75% of the time in the long run.
This concept can be visualized using reliability diagrams or calibration plots.
Reliability diagrams
Reliability Diagrams are a visual way to inspect how well the model is currently calibrated. More specifically, this diagram plots the expected sample accuracy as a function of the corresponding confidence value (softmax) output by the model.
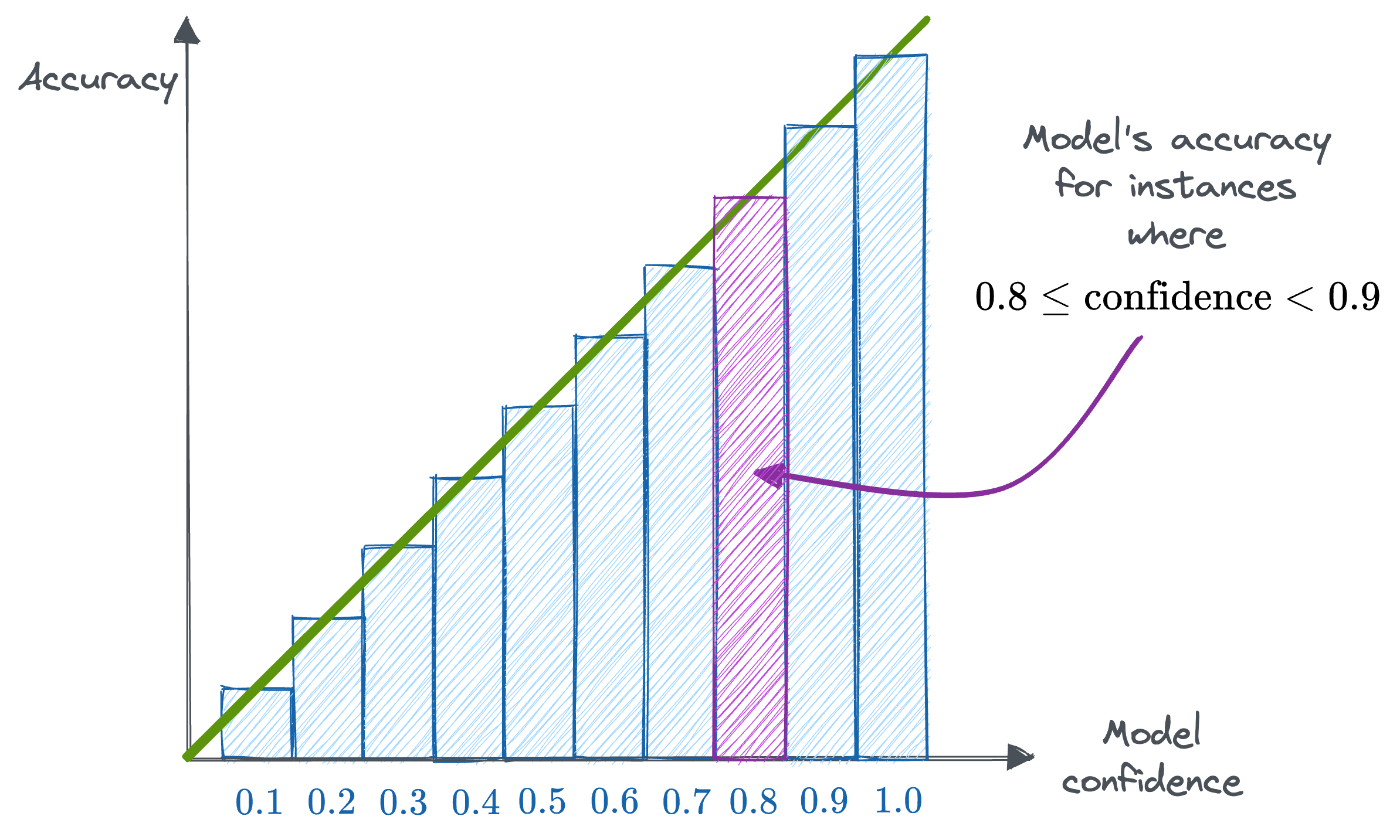
If the model is perfectly calibrated, then the diagram should plot the identity function as depicted above.
Any deviation from a perfect diagonal represents miscalibration, which is depicted below:
Read the full article
Sign up now to read the full article and get access to all articles for paying subscribers only.
Join today!