Introduction
I have had the opportunity to work on several real-world machine learning projects, both as a full-time data scientist and then as a part-time data scientist companies would outsource their data science projects to.
Building end-to-end data science and machine learning modeling projects has taught me many invaluable lessons, pitfalls, and cautionary measures that I never found anyone talking about explicitly.
To be honest, the practical lessons I am about to share in this article are something I wish someone told me when I started my career (or was progressing).
But it would be best if you didn't feel that way.
So, in this blog post, I have put down eight pitfalls you might experience and cautionary measures you can take when working on data science projects.
In my experience, these pitfalls are almost always present, but they are never that obvious to observe, which ruins many projects.
Let’s begin!
#1) Inspect decision trees
If we were to visualize the decision rules (the conditions evaluated at every node) of ANY decision tree, we would ALWAYS find them to be perpendicular to the feature axes, as depicted below:
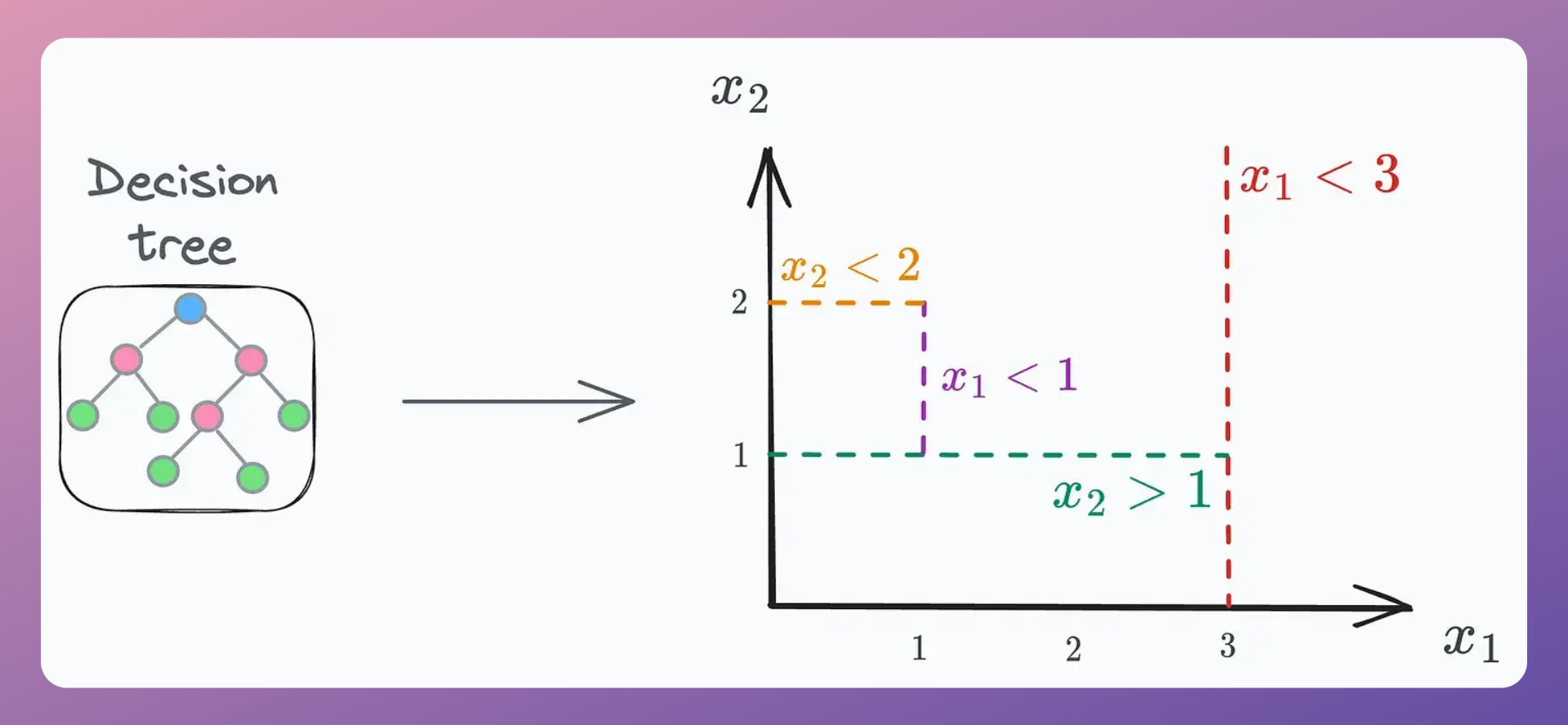
In other words, every decision tree progressively segregates feature space based on such perpendicular boundaries to split the data.
Of course, this is not a “problem” per se.
In fact, this perpendicular splitting is what makes it so powerful to perfectly overfit any dataset (read the overfitting experiment section here to learn more).
However, this also brings up a pretty interesting point that is often overlooked when fitting decision trees.
More specifically, what would happen if our dataset had a diagonal decision boundary, as depicted below:
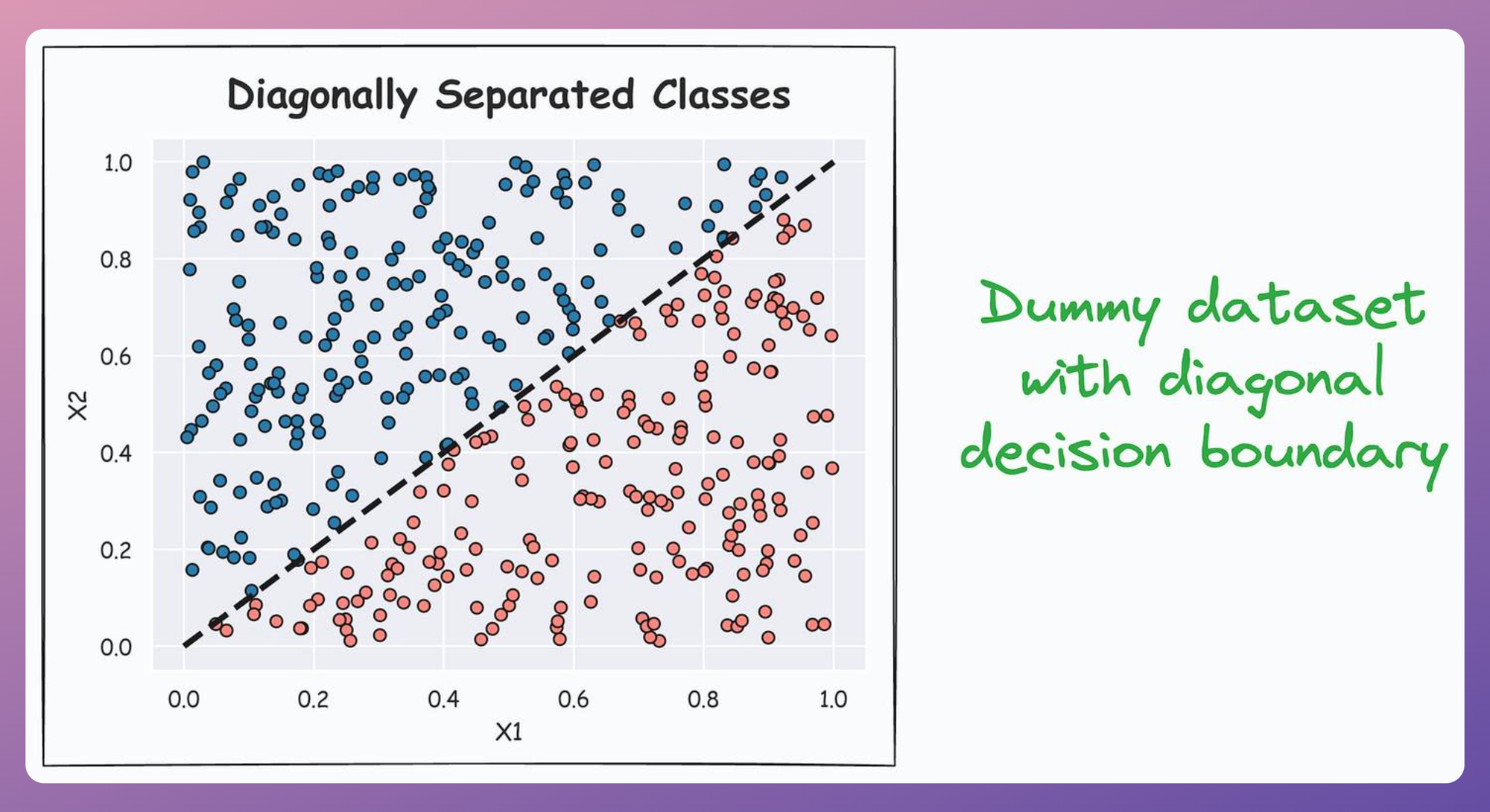
It is easy to guess that in such a case, the decision boundary learned by a decision tree is expected to appear as follows:
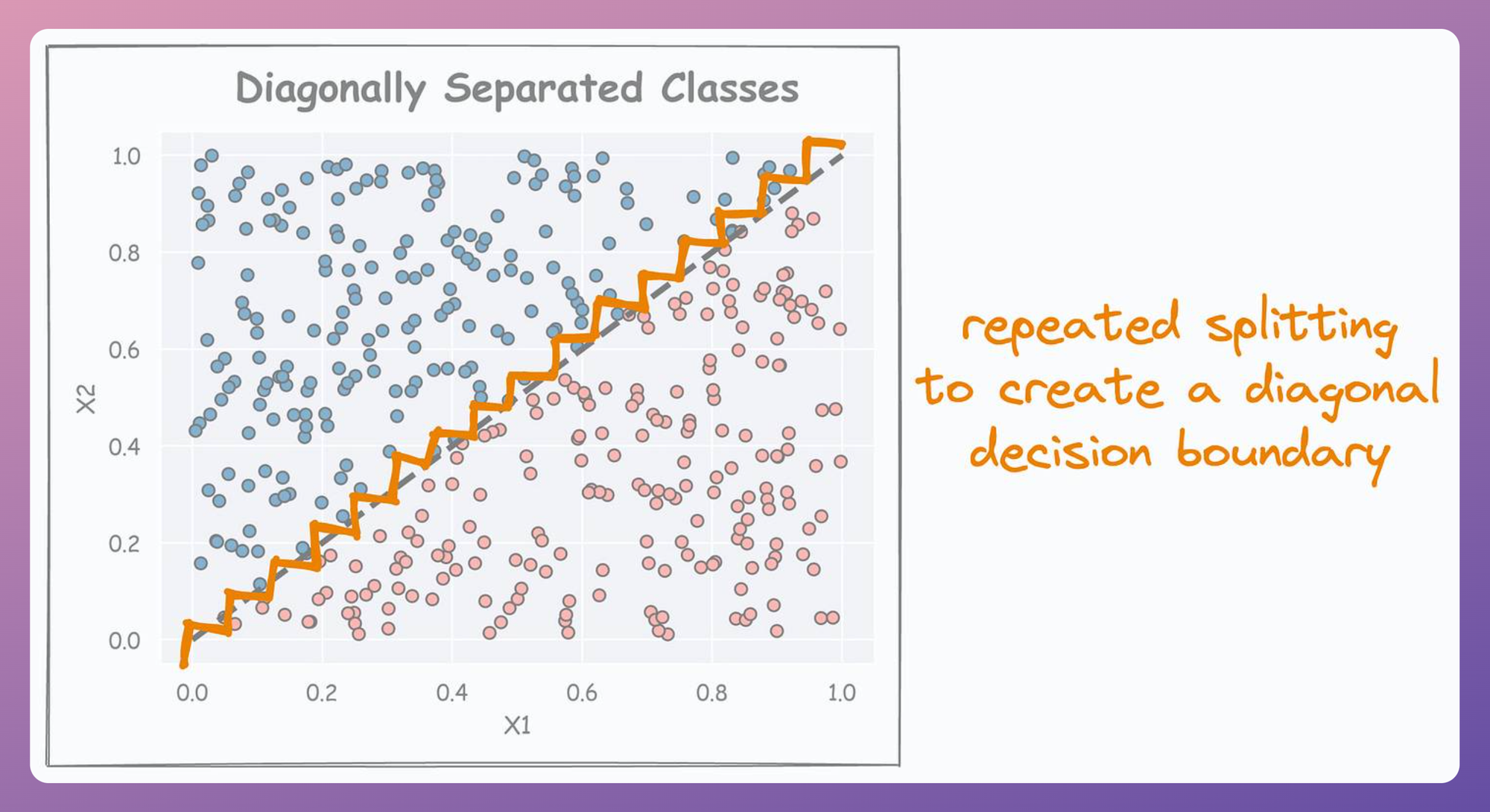
In fact, if we plot this decision tree, we notice that it creates so many splits just to fit this easily separable dataset, which a model like logistic regression, support vector machine (SVM), or even a small neural network can easily handle:
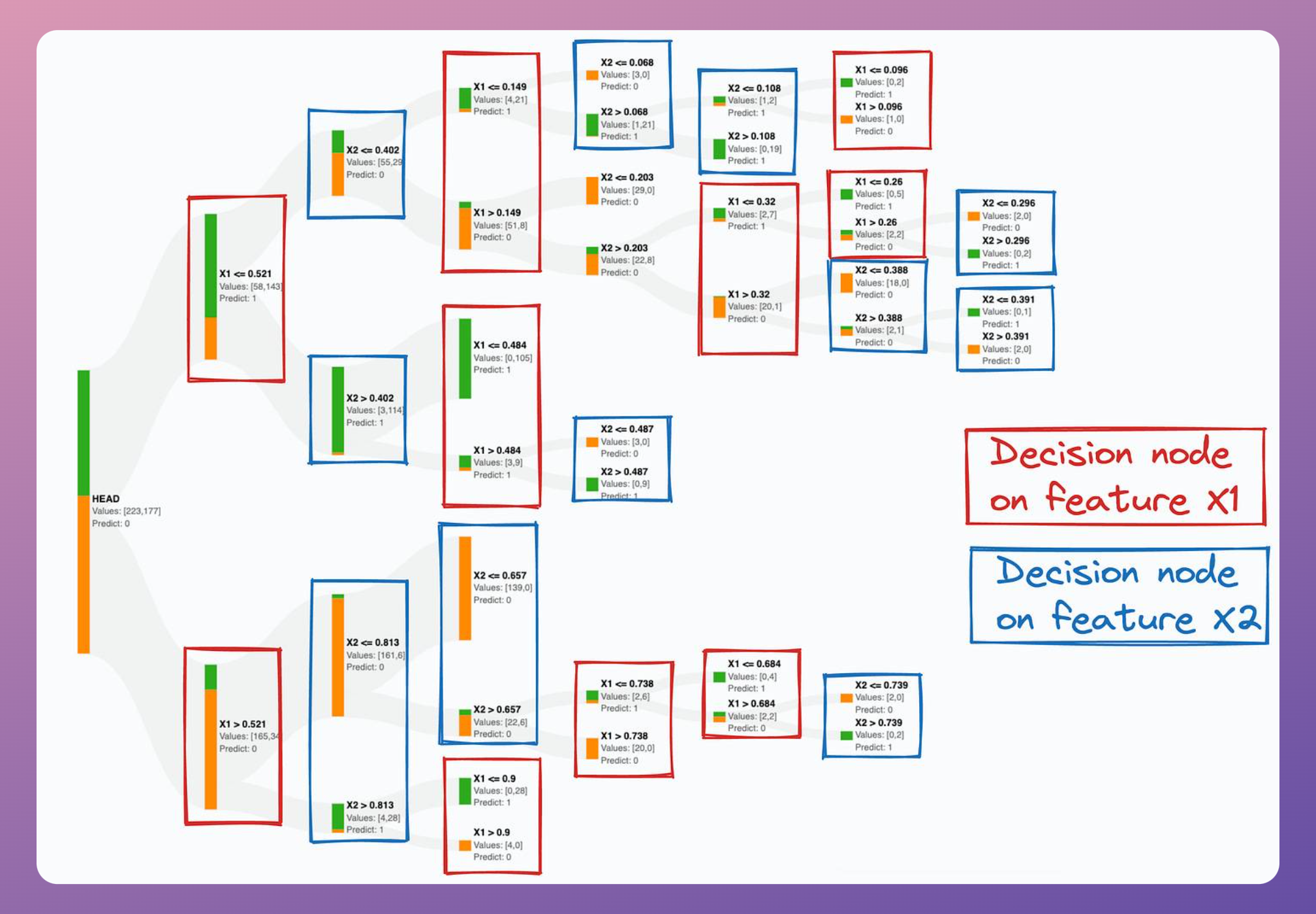
It becomes more evident if we zoom into this decision tree and notice how close the thresholds of its split conditions are:
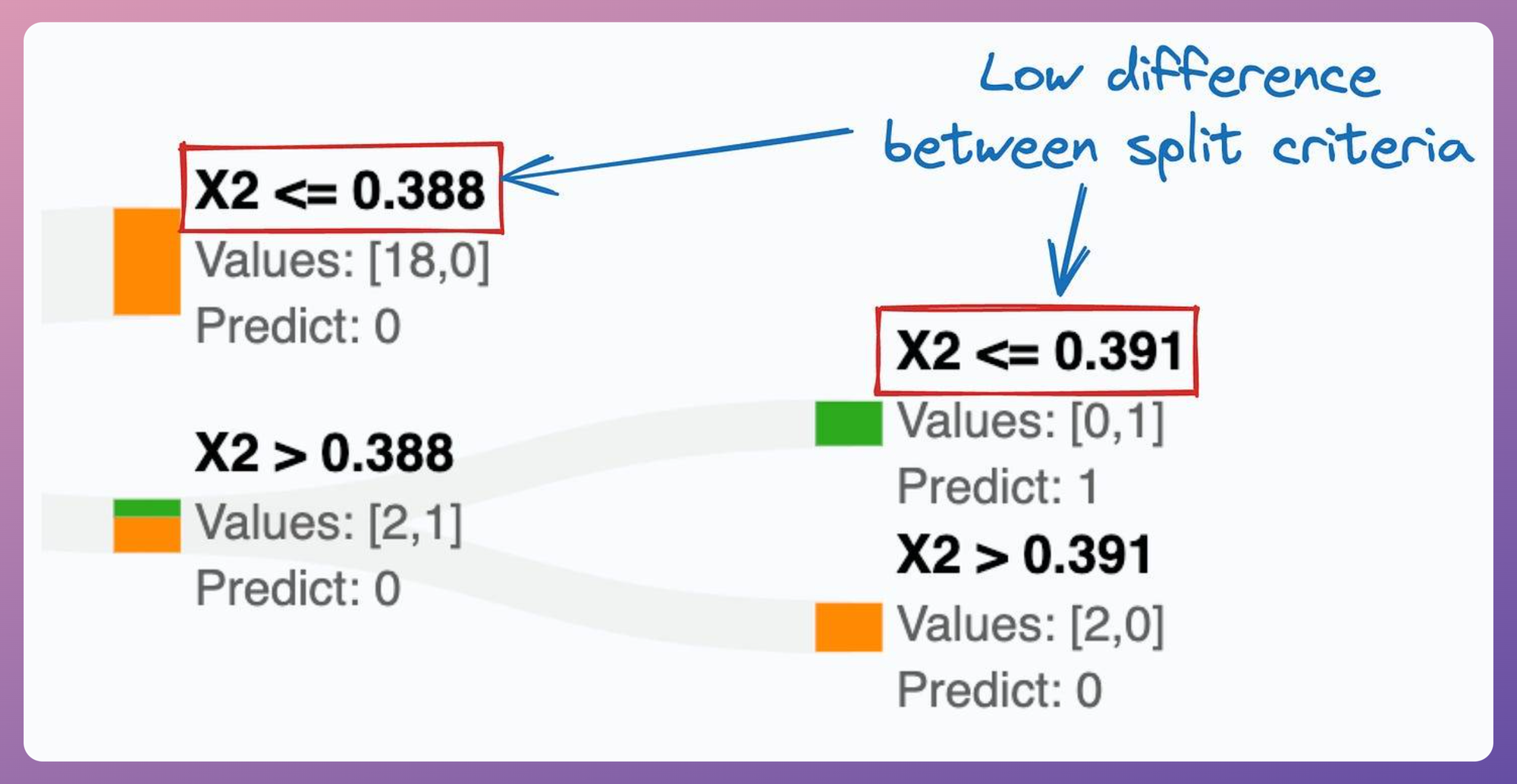
This is a bit concerning because it clearly shows that the decision tree is meticulously trying to mimic a diagonal decision boundary, which hints that it might not be the best model to proceed with.
To double-check this, I often do the following:
- Take the training data
(X, y);- Shape of
X:(n, m). - Shape of
y:(n, 1).
- Shape of
- Run PCA on
Xto project data into an orthogonal space ofmdimensions. This will giveX_pca, whose shape will also be(n, m). - Fit a decision tree on
X_pcaand visualize it (thankfully, decision trees are always visualizable). - If the decision tree depth is significantly smaller in this case, it validates that there is a diagonal separation.
For instance, the PCA projections on the above dataset are shown below:
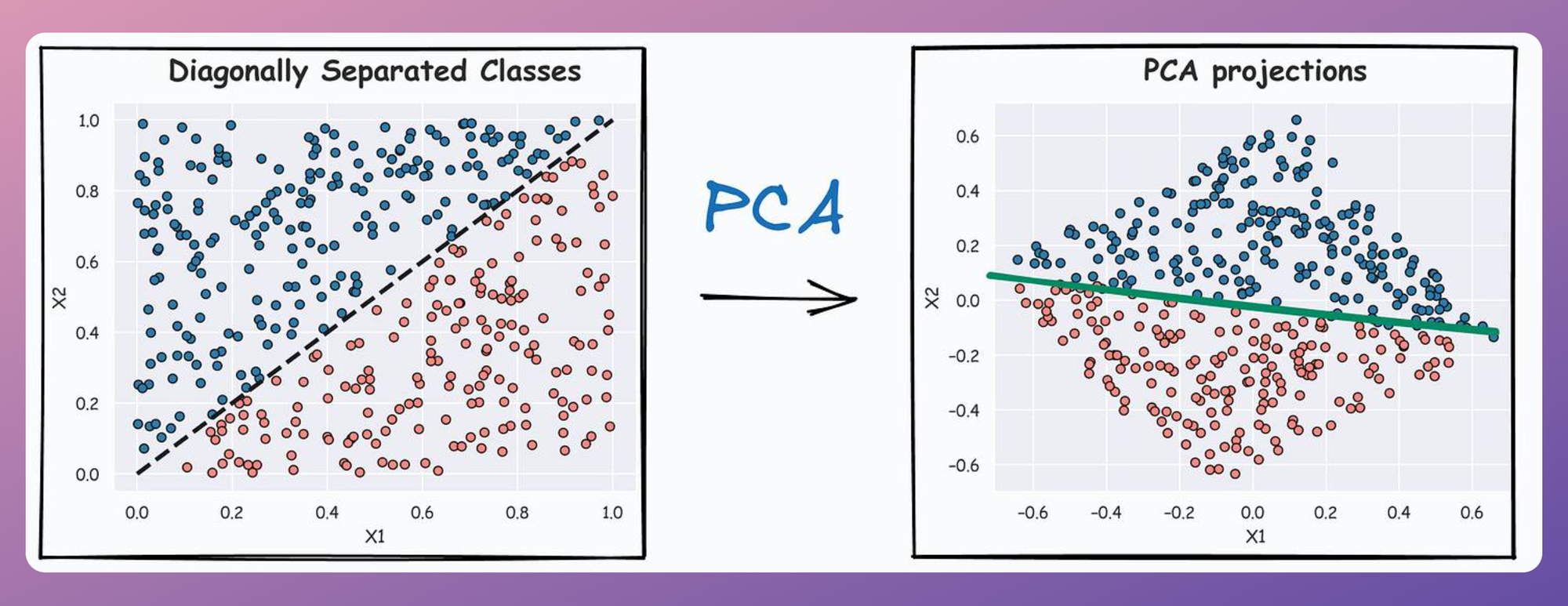
It is clear that the decision boundary on PCA projections is almost perpendicular to the X2` feature (the 2nd principal component).
Fitting a decision tree on this X_pca drastically reduces its depth, as depicted below:
This lets us determine that we might be better off using some other algorithm instead.
Or, we can spend some time engineering better features that the decision tree model can easily work with using its perpendicular data splits.
At this point, if you are thinking, why can’t we use the decision tree trained on X_pca?
While nothing stops us from doing that, do note that PCA components are not interpretable, and maintaining feature interpretability can be important at times.
Thus, whenever you train your next decision tree model, consider spending some time inspecting what it’s doing.
Of course, the objective is not to discourage the use of decision trees. They are the building blocks of some of the most powerful ensemble models we use today.
The point is to bring forward the structural formulation of decision trees and why/when they might not be an ideal algorithm to work with.
