Introduction
The true strength of a neural network comes from activation functions. They allow the model to learn non-linear complex relationships between inputs and outputs.
That is why they are considered a core component of all neural networks.
There are many activation functions one can use to learn non-linear patterns. These include Sigmoid, Tanh, etc.
But among all popular choices, many folks struggle to intuitively understand ReLU's power.
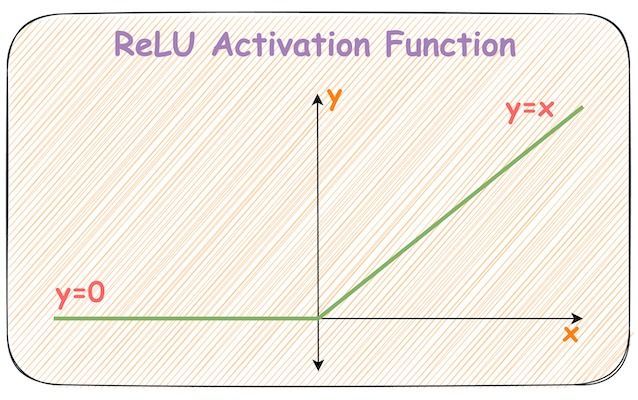
With its seemingly linear shape, calling it a non-linear activation function isn't intuitive.
An obvious question is: "How does ReLU allow a neural network to capture non-linearity?"
If you have been in that situation, let me help.
By the end of this blog, you will have an intuitive understanding of ReLU, how it works, and why it is so effective.
Let's begin!
Why activation functions?
Before understanding ReLU's effectiveness, let's understand the purpose of using activation functions.
Imagine a neural network without any activation functions.
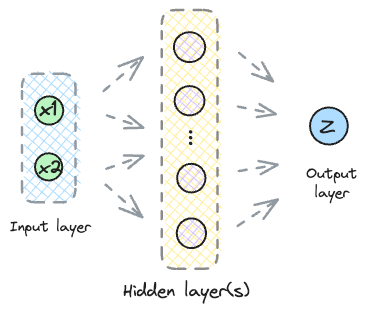
The input $x$ is multiplied by a set of weights $W_{1}$ and a bias $b_{1}$ is added.
$$ Z_{1} = W_{1} \cdot x + b_{1} $$
The above output is then passed to the next layer for transformation using a new set of weights $W_{2}$ and biases $b_{2}$.
$$ Z_{2} = W_{2} \cdot Z_{1} + b_{2} $$
This process goes on and on until the output layer.
In such a scenario, the neural network would essentially be a series of linear transformations and translations stacked together:
- First, the weight matrix $W$ applies a linear transformation.
- Next, the bias term $b$ translates the obtained output.
Thus, without activation functions, the network never captures any non-linear patterns.
To understand better, consider the following 2D dataset:
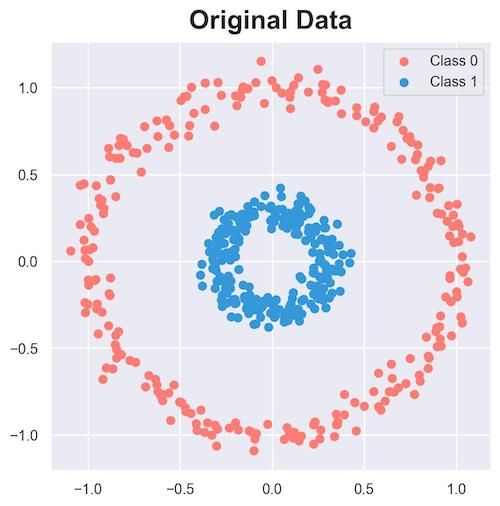
Clearly, the data is linearly inseparable.
Next, we will replicate the transformation done by a neural network. For simplicity and to create a visualization, we'll do these in 2D.
Let the weight matrix and bias be:
$$ W = \begin{bmatrix} 1 & -2 \\ -2 & 2 \\ \end{bmatrix} \ ; \ b = \begin{bmatrix} 2 \\ -1 \\ \end{bmatrix} $$
The transformation is visualized below:
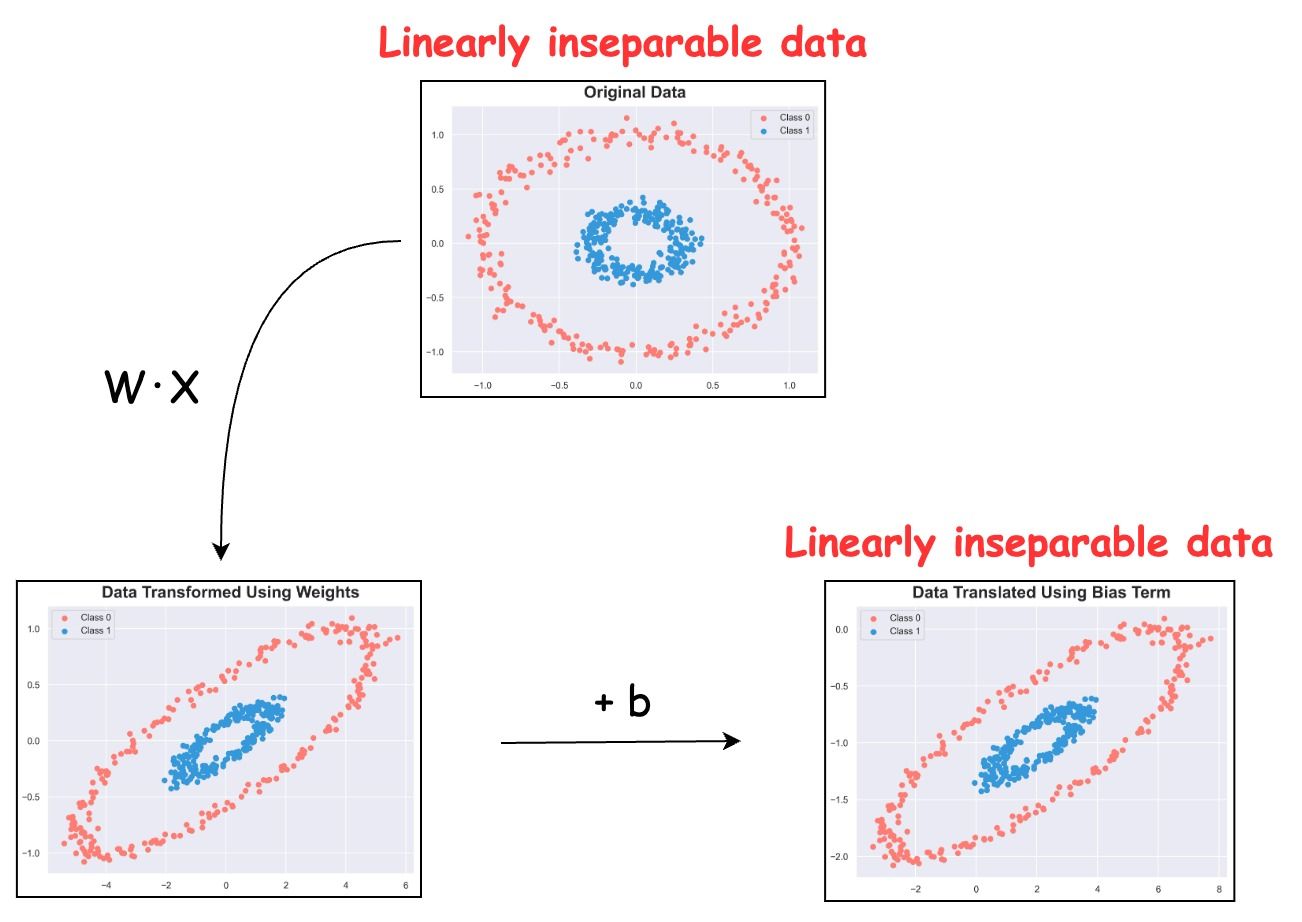
As shown, the entire transformation does nothing but scales, rotates and shifts the data. However, linear inseparability remains unaffected.
The same is true for a neural network without activations.
No matter how many layers we add, the output will always be a linear transformation of the input.
In fact, one can squish all the linear transformations into a single weight matrix $W$, as shown below:
$$ W_{k} \cdot (W_{k-1} (\dots (W_{2} \cdot (W_{1}\cdot x)))) \rightarrow Wx$$
The absence of an activation function severely limits the expressiveness and modeling power of the neural network. As a result, the network can only learn linear relationships.
We can also verify this experimentally:
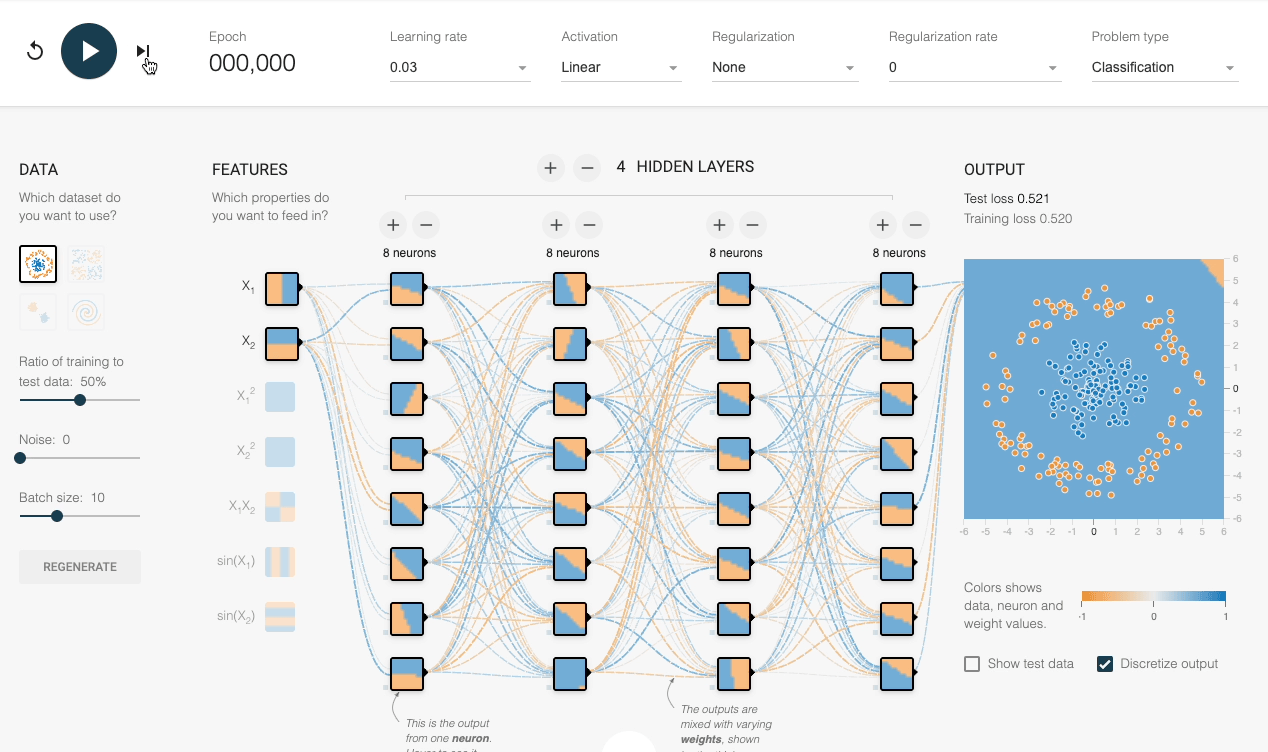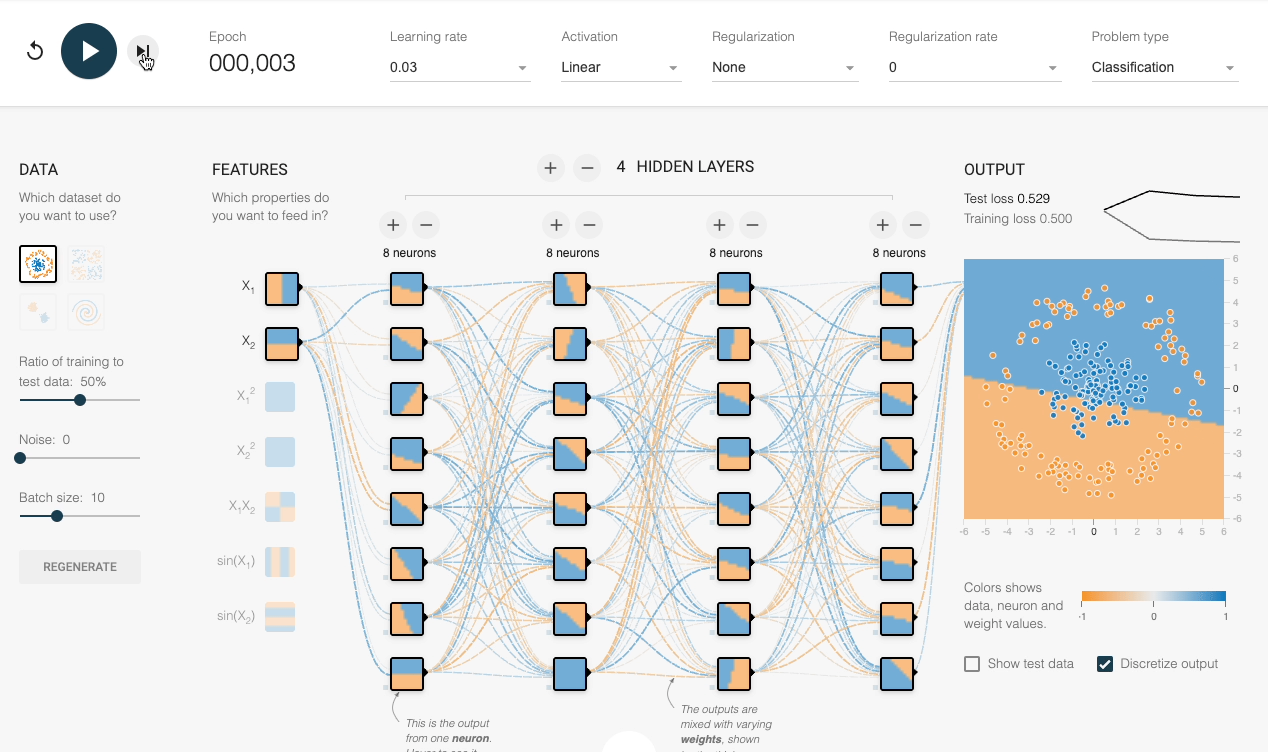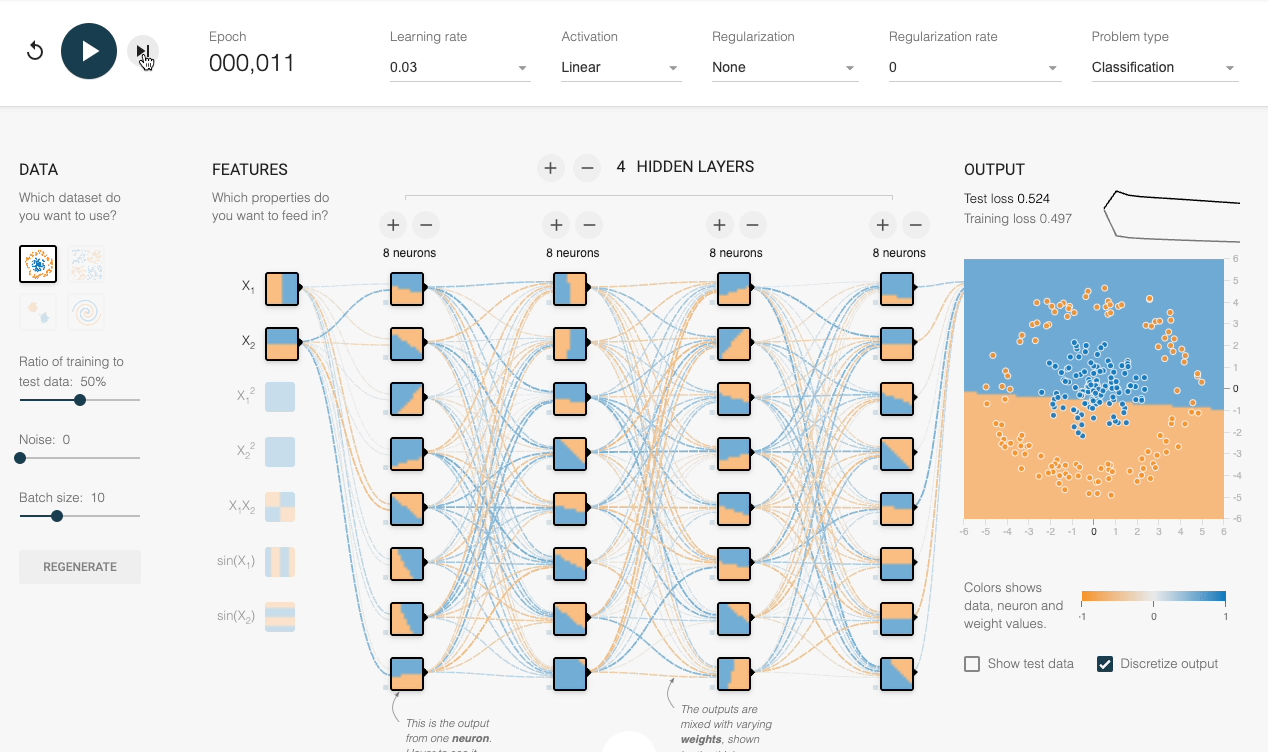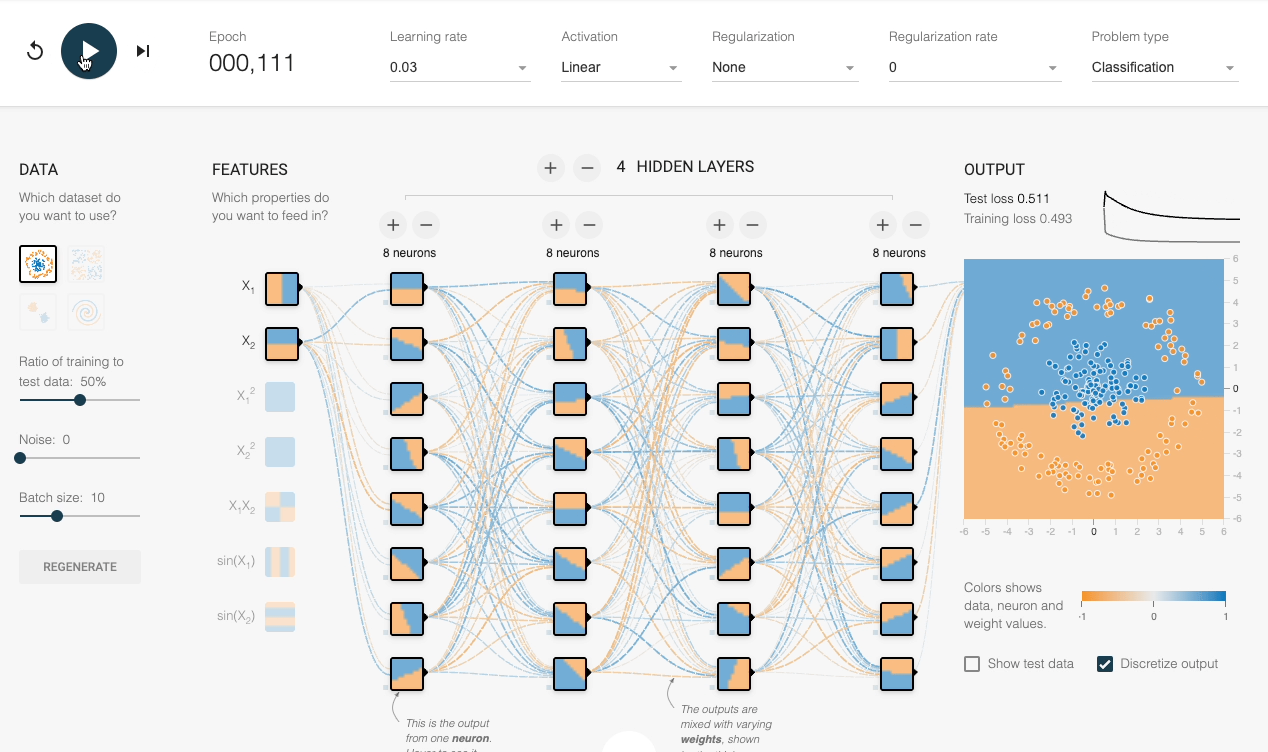
Despite having sufficient layers, each with many neurons, the decision boundary stays linear at every epoch.
However, by adding an activation function (Tanh, in this case), the network progressively learns a non-linear decision boundary:
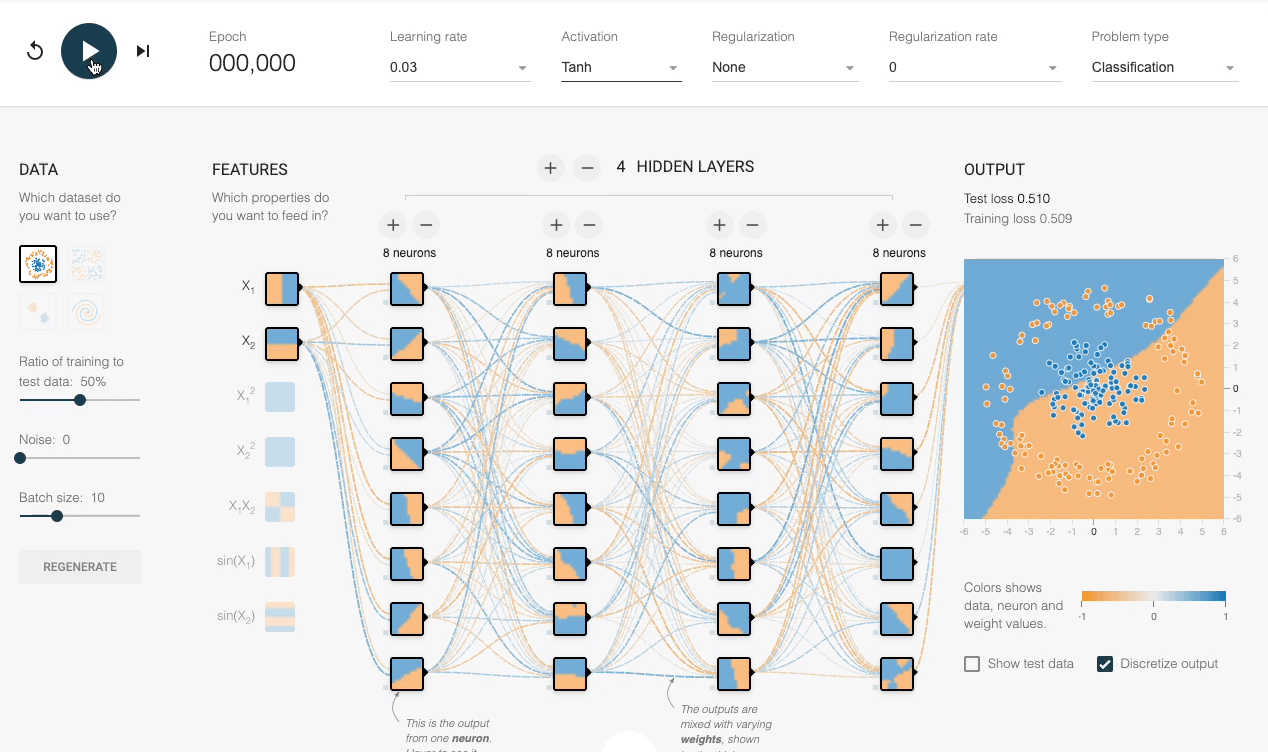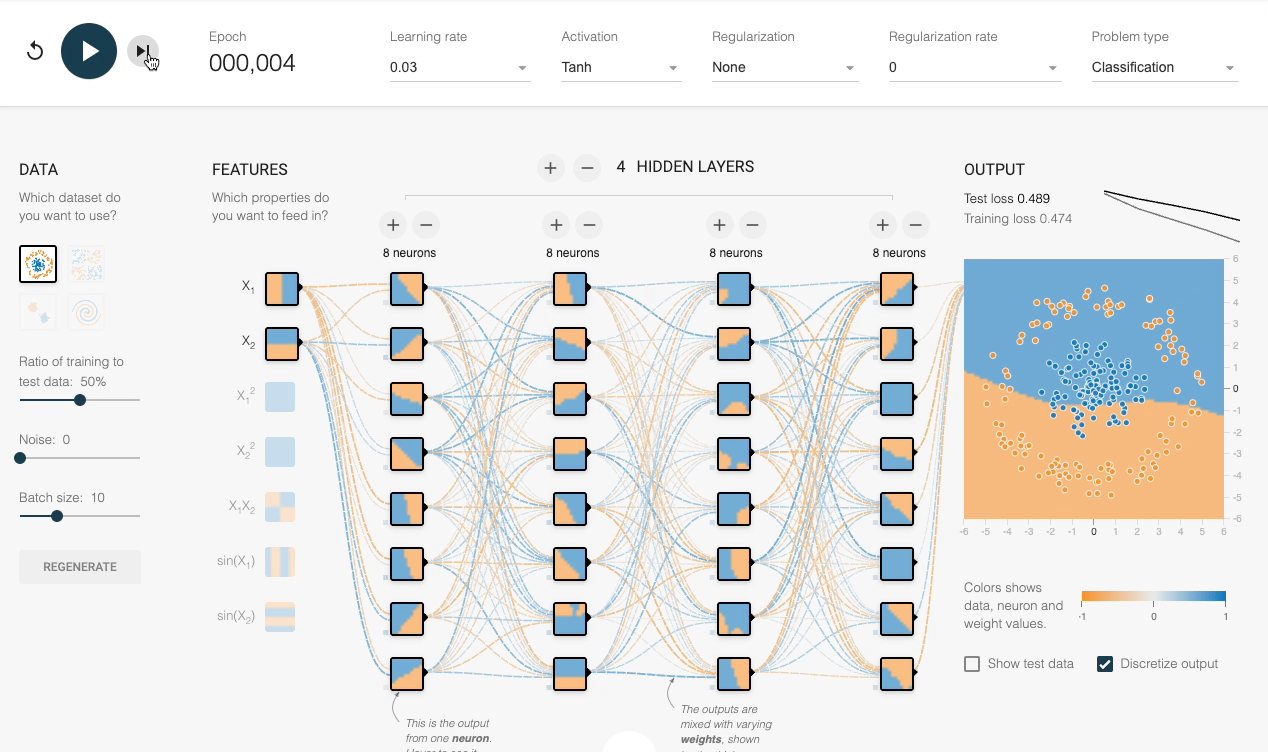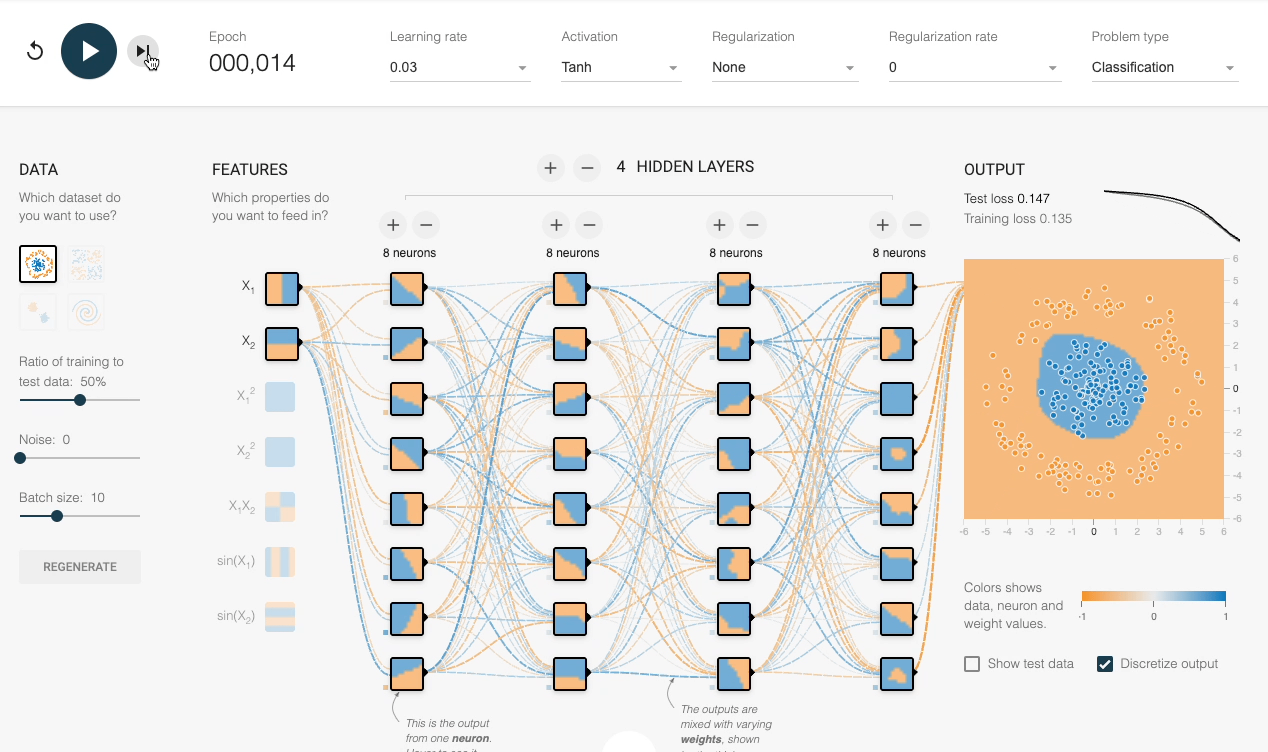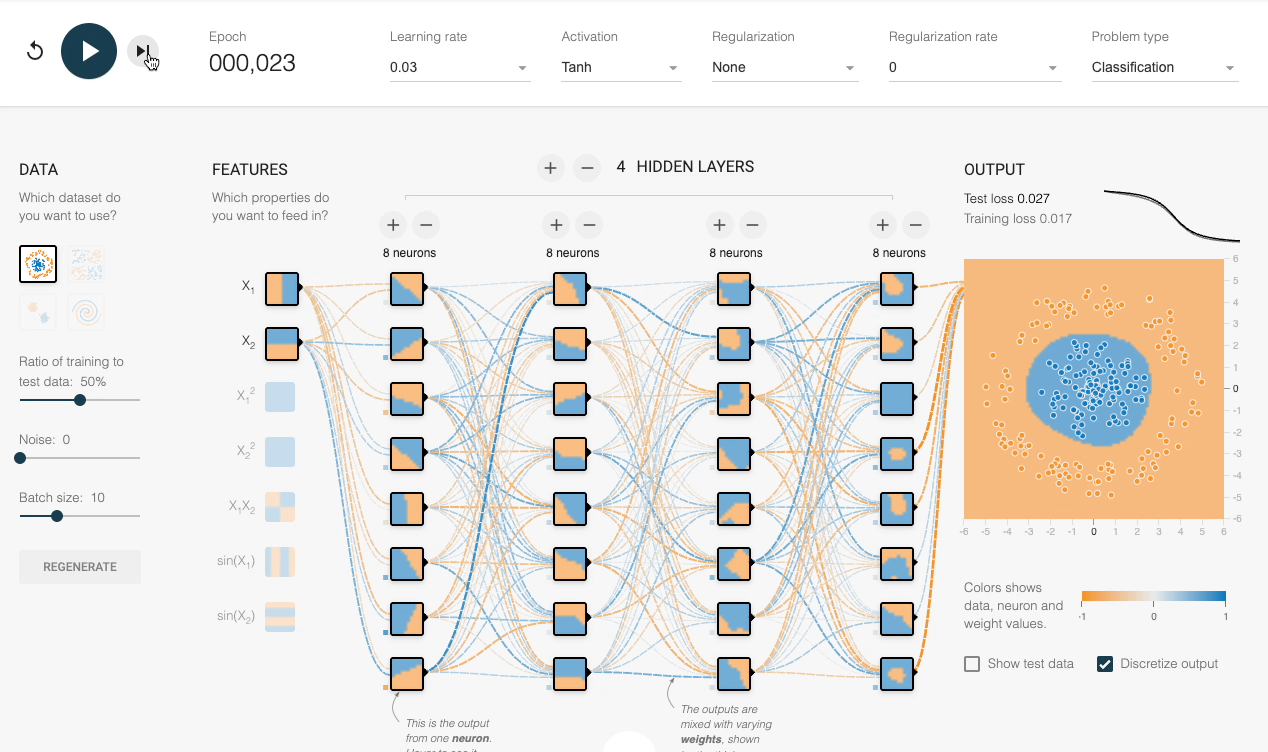
This explains the importance of activation functions.
To reiterate...
To model non-linear problems, there must be some non-linearity in the networks. Activation functions do precisely that!
Why ReLU?
Before understanding how ReLU adds non-linearity to a neural network, let's consider why we typically prefer ReLU over other activation functions.
In other words, let's look at some advantages of using ReLU over its contenders.
#1) ReLU is computationally efficient (both forward and backward)
ReLU involves a simple mathematical operation free from complex transformations such as exponentials, sinusoids, etc.
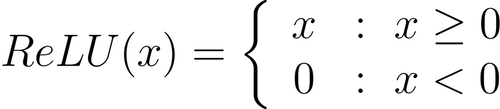
Therefore, it can be computed quickly and easily during a forward pass.
Moreover, gradient computation performed during the backward pass is equally simple.
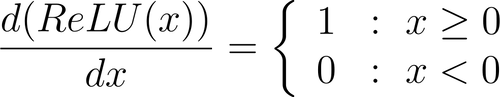
Thus, computational efficiency makes ReLU a preferred choice, especially for large neural networks with many parameters.
#2) ReLU contributes to Dropout
Overfitting is a common problem in neural networks. Dropout is a regularization technique that randomly drops (or zeros-out) units from a neural network during training.
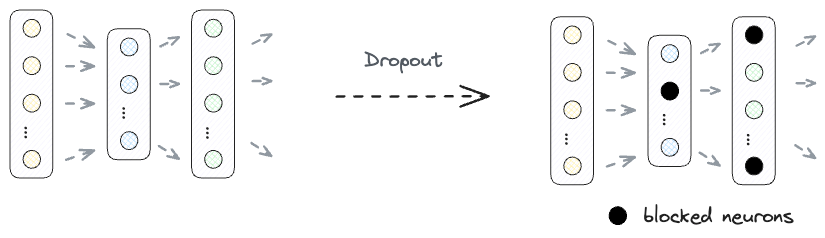
This prevents units from co-adapting excessively and encourages the network to learn more diverse and robust features.
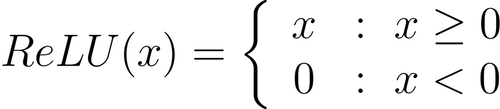
As depicted in the above equation, by using ReLU, a neuron with a negative activation is turned off.
Therefore, ReLU, in a way, contributes to Dropout and adds a bit more regularization to the network.
#3) ReLU avoids gradient vanishing
There's a common problem with activation functions such as Sigmoid (or Tanh).
At times, the gradients may become very small.
For instance, for large positive and negative inputs, the gradient of the Sigmoid curve is small.
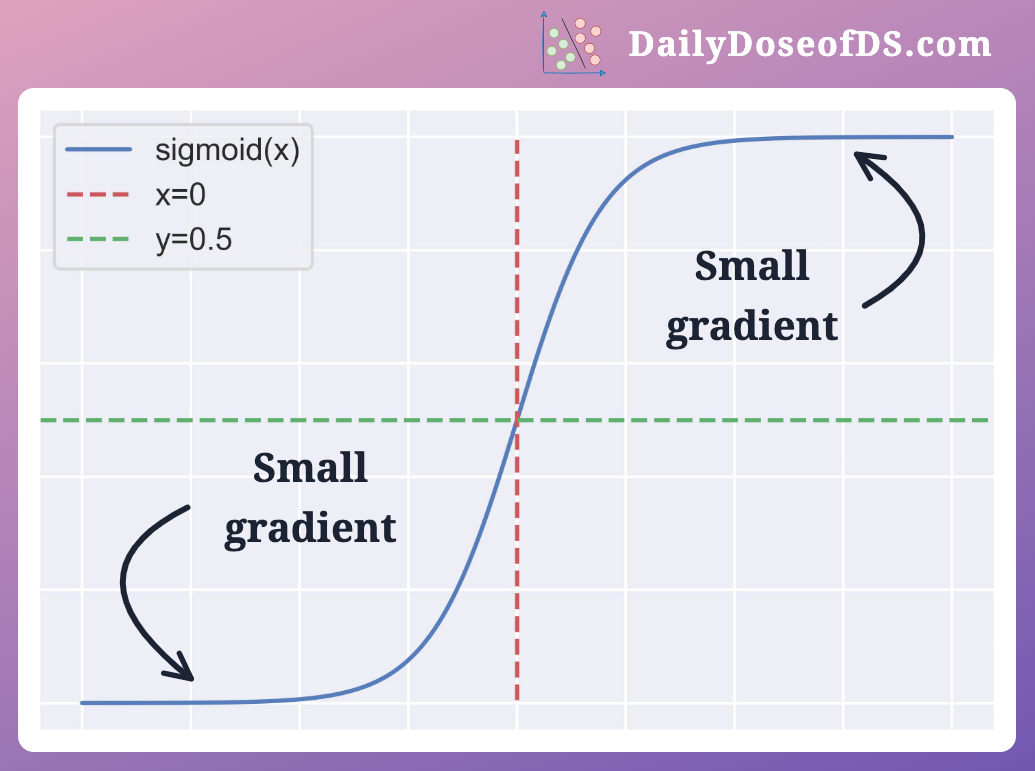
Thus, gradients may become increasingly smaller during backpropagation, leading to insignificant parameter updates.
Vanishing gradients make it difficult for the network to learn, especially the initial layers of the network.
ReLU, on the other hand, produces a constant gradient for positive inputs, thereby avoiding vanishing gradients.
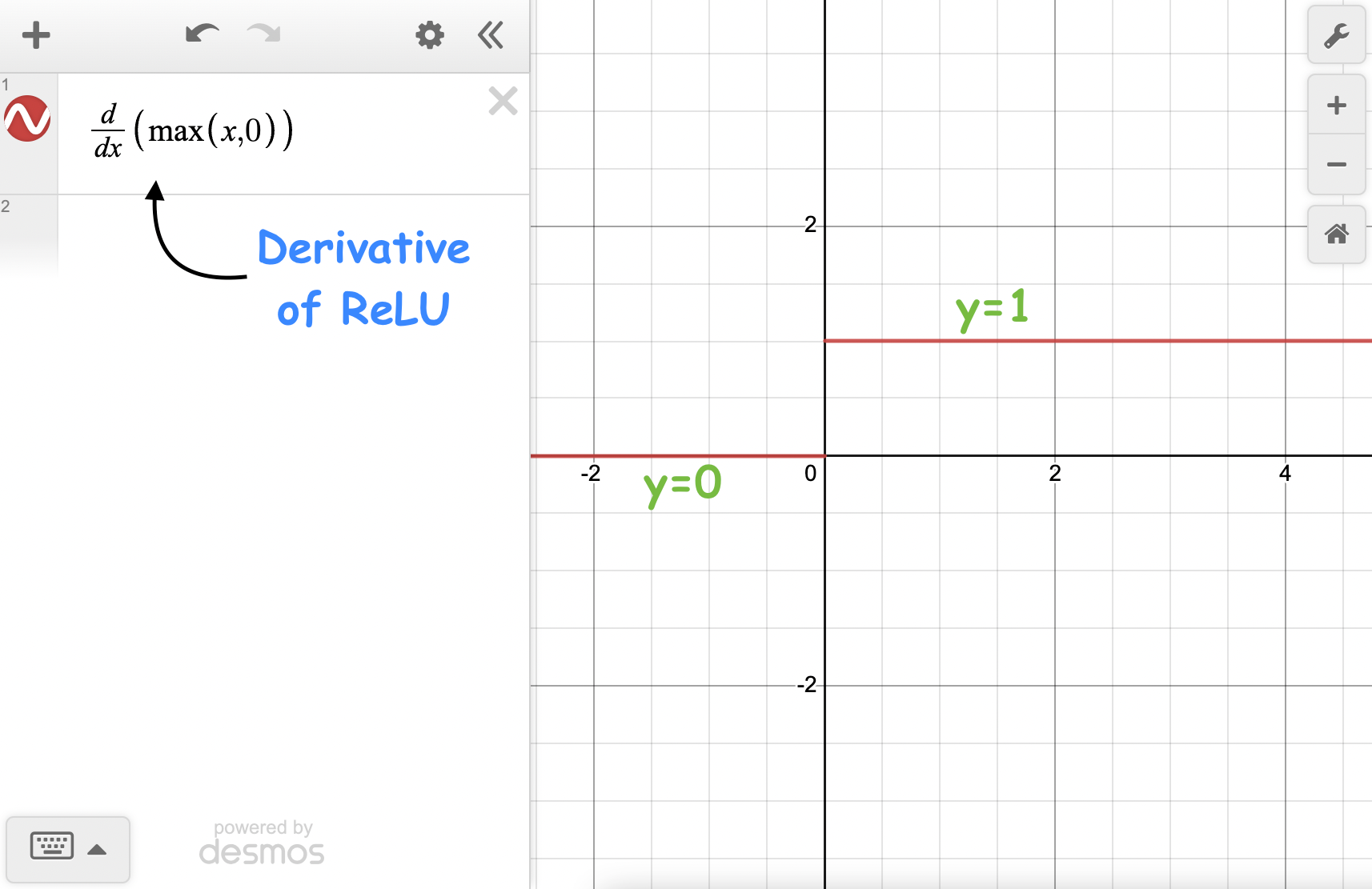
This results in faster learning.
Proof
Now that we understand what makes ReLU advantageous over other activation functions, we'll see how ReLU acts as a non-linear activation function.
