A Mathematical Deep Dive Into the Curse of Dimensionality

Introduction

If you are reading this, it's pretty likely you would have heard of the term “curse of dimensionality.”

It's totally okay if you don't fully understand it yet since that is the purpose of this article.

But in my experience, most people find it quite confusing to understand what it actually means and what is the origin of the curse of dimensionality.

I vividly remember when I first heard about it, I was pretty confused and couldn't grasp what it actually meant since the resources/posts/tutorials I mostly heard and learned it from never cared to dive into the mathematical details explaining the idea, and instead was mostly assumed as a given.

Also, I was confused since dimensionality itself didn’t seem like a bad thing at all. In fact, having more dimensions meant I had more features in my dataset, more data to train my model, and potentially more complex insights to extract.

So, I had several questions:

• What it actually is?
• Why is it called a “curse”?
• What's the mathematical reasoning behind it?
• And more.

Think about it.

We, specifically Richard Bellman, in 1961, first coined it. At that time, he had no idea this was a problem, and no one else in the machine learning community knew about the curse of dimensionality, correct?

Thus, in my opinion, an ideal answer should formulate it from scratch and with valid reasoning, replicating the exact thought process when it was first discovered, which means that one should NOT know anything about it beforehand.

As you will see shortly, the truth is that the curse of dimensionality affects a range of areas in machine learning and data science, from distance metrics to model generalization, and in this deep dive, I intend to leave you with an explanation uncovering every piece of mathematical intuition behind it.

Also, to make this discussion engaging, we shall not solely focus on theory. Instead, we will use Python to generate and explore high-dimensional datasets, allowing us to observe the practical implications of the curse of dimensionality firsthand.

Let's begin!

Why dimensionality creates problems?

Having understood the curse of dimensionality pretty well now, the reason why I think people find it difficult to understand it is that our imagination is limited to three dimensions.

If we go to any dimension beyond that, we lose track of what that high-dimensional space would look like.

Moreover, for simplicity, we often assume that geometrical properties and concepts we utilize in one, two, and three dimensions behave similarly in higher-dimensional spaces. 

As we will find out shortly, this is NEVER the case.

In other words, as dimensionality increases, we start observing several convoluted and counterintuitive phenomena that aren't apparent in low dimensions.

The curse of dimensionality primarily stems from how dimensionality impacts volume, which has profound implications for data distribution.

There are a couple of ways to explain this.

Explanation #1

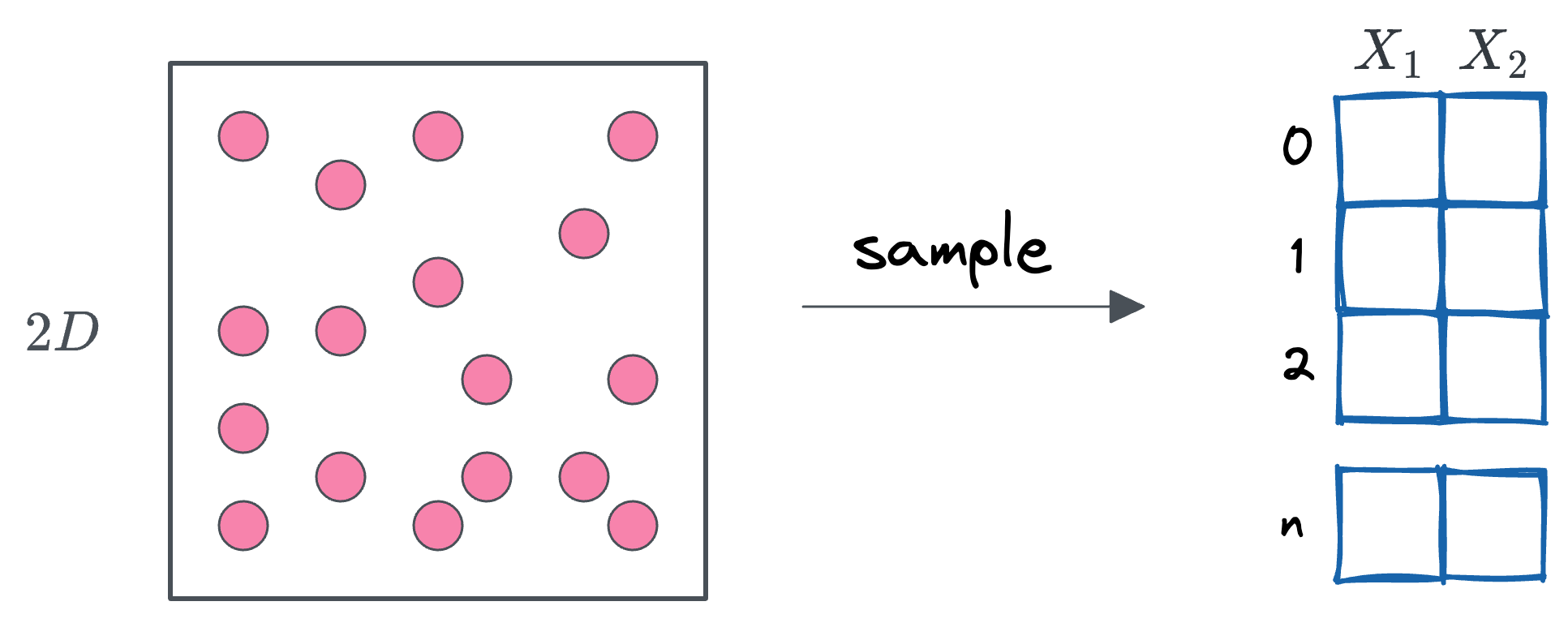
Imagine a dataset as a random sample drawn from a population. For simplicity, picture the population as a set of points within a square.

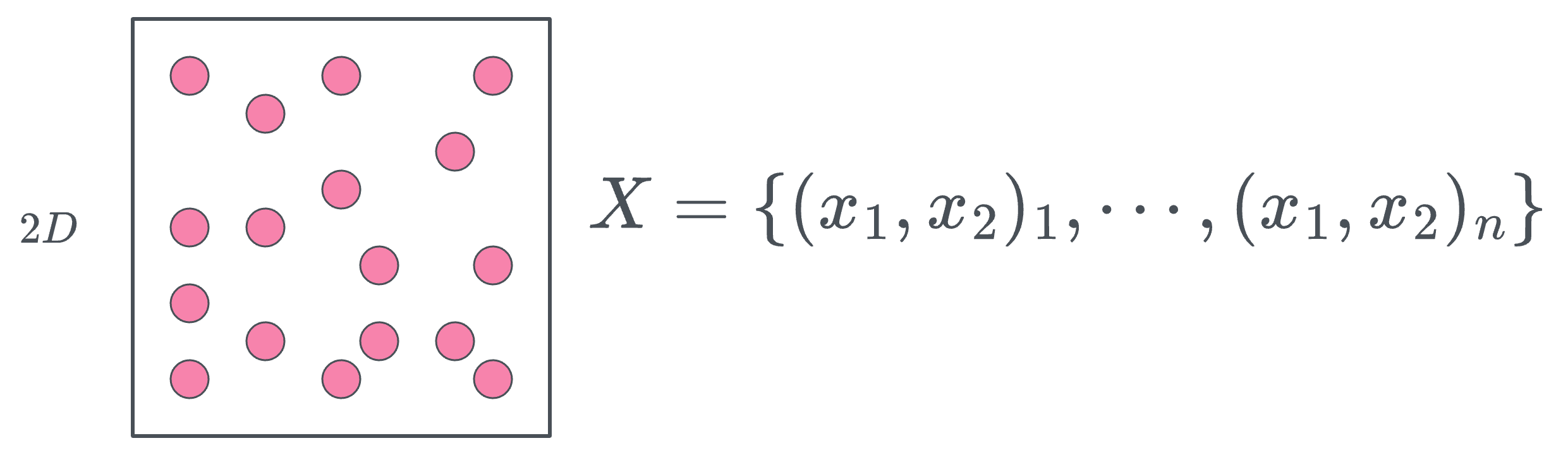
This square represents all points $(x_1, x_2)$ such that $0 \leq x_1 \leq 1$ and $0 \leq x_2 \leq 1$, with a side length of 1.

Now, if we assume the points are uniformly distributed across the square, it means that every point within this space has an equal probability of being selected.

When we randomly select a sample of size $n$ from this population, the resulting dataset has $n$ rows and two features—since each point has two coordinates, $x_1$ and $x_2$. Thus, the dataset exists in a 2-dimensional space.

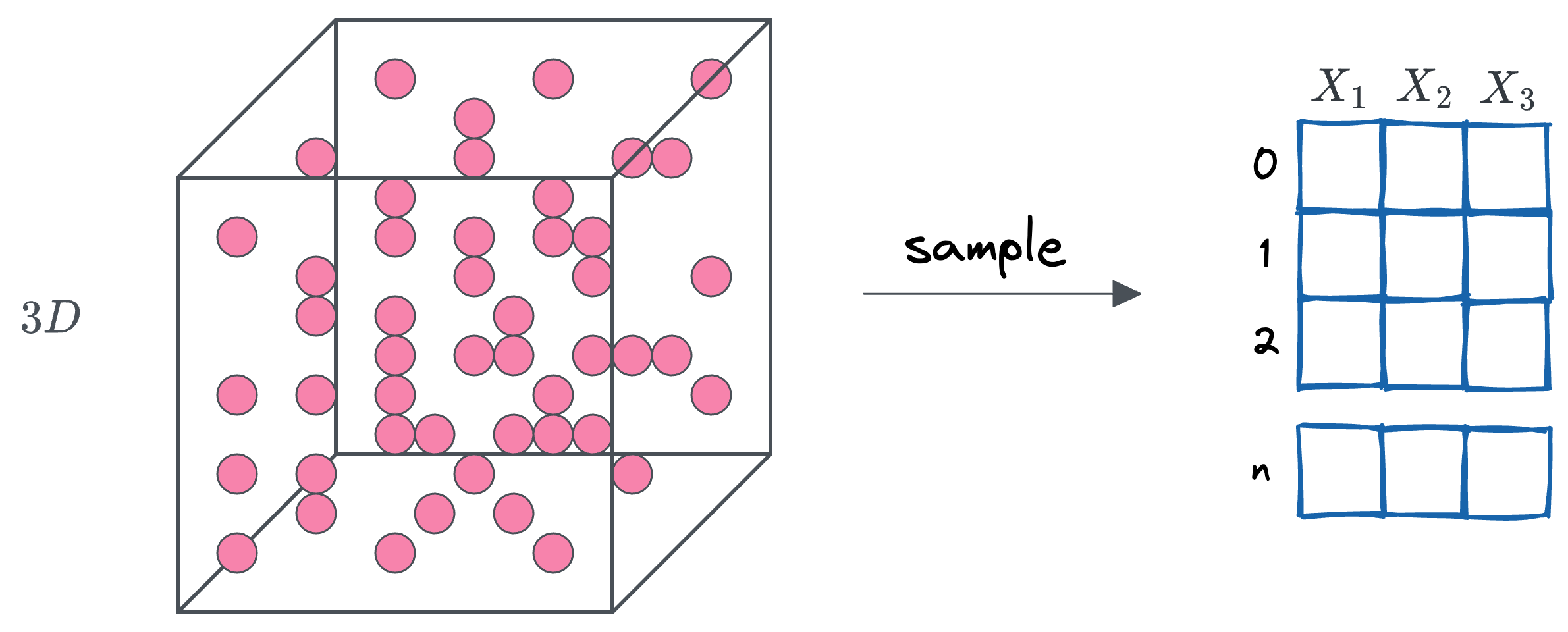
In a similar way, we can construct a three-dimensional dataset by randomly sampling points from a cube with edge length 1.

This cube encompasses all points $(x_1, x_2, x_3)$ such that $0 \leq x_1 \leq 1$, $0 \leq x_2 \leq 1$, and $0 \leq x_3 \leq 1$, and we assume these points are uniformly distributed within the cube. The result is a dataset with $n$ samples, each represented by three features corresponding to the coordinates in 3D space.

Extending this concept further, we can create a $d$-dimensional dataset by drawing random samples from a $d$-dimensional hypercube with an edge length of 1 (which can't be visualized, of course).

This hypercube contains points defined as $(x_1, x_2, \dots, x_d)$, where $0 \leq x_i \leq 1$ for all $i = 1, \dots, d$.

Similar to the 2D and 3D cases, the points are uniformly distributed within the hypercube. The resulting dataset will consist of $n$ examples, each described by $d$ features corresponding to the coordinates in $d$-dimensional space.

Now, the volume of a $d$-dimensional hypercube with an edge length $L$ is given by $L^d$.

Since in our case, $L = 1$, the total volume of the hypercube remains 1, regardless of the value of $d$.

However, what’s crucial here is not the total volume but how that volume is distributed across the hypercube as dimensionality increases.